London Institute in 2021
2021 was transformative for the London Institute. We hired new talent, published pioneering research and moved into Faraday's rooms at the Royal Institution. We also compiled a list of the top 23 mathematical challenges of our time, to remind ourselves and others to aim high.
The London Institute is now located at the Royal Institution in Mayfair. It was here that Sir Humphry Davy identified nine elements of the periodic table and Michael Faraday uncovered the principles of electromagnetism. There could be no more inspiring place for us to work.
Our papers span five main research themes, from mathematics that unifies to the theory of human enterprise. Our output exceeded that of the previous year by 41%, part of our plan to double it every two years. We concentrate on the quality of our papers and not just the quantity.
FC
FS
FL Science AdvancesBreaking classical barriers
Circuits of memristors, resistors with memory, can exhibit instabilities which allow classical tunnelling through potential energy barriers.
PVTGGC
Physical Review ECoexistence in diverse ecosystems
Scale-invariant plant clusters explain the ability for a diverse range of plant species to coexist in ecosystems such as Barra Colorado.
AAOD
LM New Journal of PhysicsGoing, going, gone
A solution to the information paradox uses standard quantum field theory to show that black holes can evaporate in a predictable way.
CJAM
AA Journal of Mathematical BiologyTumour infiltration
A delicate balance between white blood cell protein expression and the molecules on the surface of tumour cells determines cancer prognoses.
MB
PB
SBFCGC... Nature Reviews PhysicsPhysics of financial networks
Statistical physics contributes to new models and metrics for the study of financial network structure, dynamics, stability and instability.
YLDEFLOD
New Journal of PhysicsQuick quantum neural nets
The notion of quantum superposition speeds up the training process for binary neural networks and ensures that their parameters are optimal.
OFYH
JRYXFY Journal of High Energy PhysicsQFT and kids’ drawings
Groethendieck's “children’s drawings”, a type of bipartite graph, link number theory, geometry, and the physics of conformal field theory.
AM
FAMSFA
AC
Physical Review EExact linear regression
Exact methods supersede approximations used in high-dimensional linear regression to find correlations in statistical physics problems.
SMHŠGC
VZ Physical Review ERisky bank interactions
Networks where risky banks are mostly exposed to other risky banks have higher levels of systemic risk than those with stable bank interactions.
YH
International Journal of Modern Physics AUniverses as big data
Machine-learning is a powerful tool for sifting through the landscape of possible Universes that could derive from Calabi-Yau manifolds.
Cancer and coronavirus
Cancer patients who contract and recover from Coronavirus-2 exhibit long-term immune system weaknesses, depending on the type of cancer.
PB
TMLS Journal of Financial StabilityChannels of contagion
Fire sales of common asset holdings can whip through a channel of contagion between banks, insurance companies and investments funds.
True scale-free networks
The underlying scale invariance properties of naturally occurring networks are often clouded by finite-size effects due to the sample data.
TF
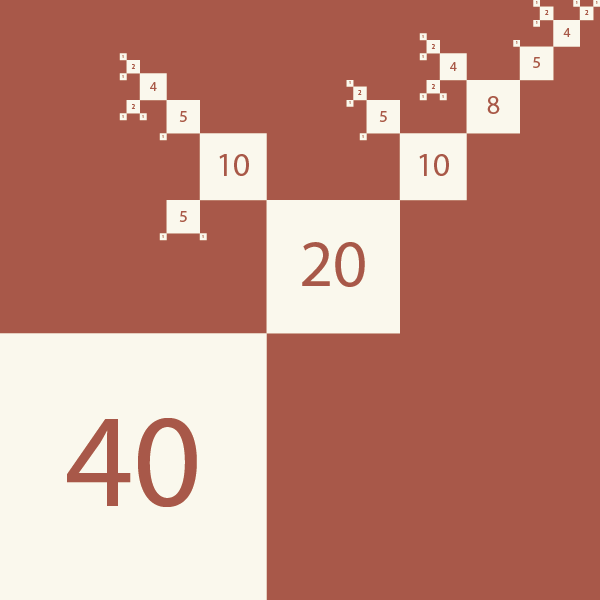
Arxiv for Journal of Number TheoryAmple and pristine numbers
Parallels between the perfect and abundant numbers and their recursive analogs point to deeper structure in the recursive divisor function.
STIT
ArxivScale of non-locality
The number of particles in a higher derivative theory of gravity relates to its effective mass scale, which signals the theory’s viability.
TF
Sub. to Nature AgeingI want to be forever young
The mortality equation governs the dynamics of an evolving population with a given maximum age, offering a theory for programmed ageing.
BKIS
ISAZ Journal of the Institute of Mathematics of Jussieu, in press Energy bounds for roots
Bounds for additive energies of modular roots can be generalised and improved with tools from additive combinatorics and algebraic number theory.
TF
Sub. to Proceedings of the National Academy of Sciences of the USABiological logics are restricted
The fraction of logics that are biologically permitted can be bounded and shown to be tiny, which makes inferring them from experiments easier.
TF
IT Arxiv for Science AdvancesRecursive structure of innovation
A theoretical model of recursive innovation suggests that new technologies are recursively built up from new combinations of existing ones.
Our events included a talk about the Theory of Everything, a conversation with Sir Roger Penrose and a workshop to figure out the top 23 mathematical challenges. Our new home in the Royal Institution provides us with the space and reach to attract larger audiences than ever.
Lectures13 Dec 2021
Science of storytelling
Prof. Alison Woollard explores the science of storytelling and storytelling in science—a neglected virtue in modern scientific research.
Ri Lecture1 Dec 2021
Theory of Everything
Professor Yang-Hui He tells the captivating story of the holy grail of science: the mathematical quest for a unifying theory of everything.
Ri Lecture26 Oct 2021
Talking to Penrose
Sir Roger Penrose talks about physics, philosophy and art in a conversation with Thomas Fink and Yang-Hui He in the Faraday lecture theatre.
Lectures27 Sep 2021
Maths and machines
Conrad Wolfram describes how two brothers harnessed machines to do mathematics, changing the way we think about computational thinking.
Alumni event22 Sep 2021
Cheers, Brits and Yanks
Princeton and Caltech alumni celebrate Faraday’s birthday at the London Institute for Mathematical Sciences, inside the Royal Institution.
Discussions21 Sep 2021
In search of serendipity
The London Institute is hosting a lunch at the Royal Institution to promote serendipity between leaders in business, finance and physics.
Conferences1–13 Aug 2021
Mathematical Dialogues
Yang-Hui He co-organises the Nankai Symposium on dialogues between mathematics and physics, with the plenary talk by Sir Roger Penrose.
Workshops20 Jun 2021
Greek week
What is the limit to human achievement? To find out, we sent a team to a Greek island for a week to immerse themselves in a single problem.
Workshops26 Mar 2021
23 mathematical challenges
A one-day symposium of physicists and mathematicians to write down a list of the 23 most important mathematical challenges of our time.
Our perspectives are essays that express the London Institute’s interests and point of view, while contributing to the national debate on how to fund and carry out science. They include opinion pieces in The Times, The Spectator, Science in Parliament and The Daily Telegraph.
THE SPECTATOR
Why we must boldly go
The human impulse to look beyond the horizon, “to boldly go where no man has gone before”, leads us to the most transformative discoveries.
THE TIMES
23 mathematical challenges
To mark the launch of ARIA, which aims to tackle the toughest problems, we made a list of the top 23 mathematical challenges of our time.
THE DAILY TELEGRAPH
The intelligent organisation
Showing up for work makes organisations more intelligent, because it let’s workers switch between focus and interaction in an unplanned way.
THE SPECTATOR
Britain’s version of DARPA
As the government creates its Advanced Research and Invention Agency, it could learn from the exceptional history of the Royal Institution.
Move to the Royal Institution
The London Institute has moved into the iconic Royal Institution, where it will expand its programme of curiosity-driven theoretical science.
SCIENCE IN PARLIAMENT
Independent science
Supporting non-university research institutes with core funding will finally give aspiring researchers an alternative to a university job.
The people we employ range from writers to researchers and financiers to physicists, since a top-class institute requires scientists and support staff alike. We recruited two researchers, a string theorist and a biophysicist, and our first Finance Director and Development Director.
Former finance director
Ali Emamy
Mr Emamy is the Finance Director for LIMS and LIMS Ventures. He was previously CFO at Nest Corporation and several financial services firms.
Development
Sarah Myers Cornaby
Mrs Myers Cornaby is the LIMS Development Director, where she has raised funds for our Arnold and Landau posts and is growing our endowment.
Statistical physics
Forrest Sheldon
Dr Sheldon is a Junior Fellow at LIMS, following a physics postdoc at Los Alamos. He works on mathematical biology and neural computing.
Mathematical physics
Yang-Hui He
As well as a Fellow at LIMS, Prof. He is a professor of physics at the University of London. He works on string theory and machine learning.