Any irreducible fraction can be uniquely represented as a regular continued fraction. From the theory of continued fractions, Zaremba’s famous 1971 conjecture posits that every integer appears as the denominator of a finite continued fraction whose partial quotients are bounded by an absolute constant. Zaremba himself conjectured that the value of this absolute constant equals 5. Two decades later, Hensley conjectured that for a large, prime denominator a bound equal to 2 is sufficient. Ever since, further tightening this bound has been an ongoing problem in the number theory community.

In this seminar, Prof. Ilya Shkredov presents a marked improvement to the well-known Korobov bound on Zaremba’s conjecture. In 1963, using exponential sums, Korobov proved that for any prime denominator, there exists a coprime numerator such that the partial quotients of the continued fraction expansion never exceed the log of the denominator. Shkredov presents a proof that, for any sufficiently large prime denominator q, all partial quotients never exceed O(log q/log log q). The same result takes place for composite q.

## Event info
---
This seminar takes place on Wednesday 29 March 2023 at 5 pm in Tyndall’s Parlour at the London Institute, on the second floor of the Royal Institution in Mayfair. The seminar will be followed by drinks and refreshments onsite. To register to attend, please email at@lims.ac.uk.


Prof. Ilya Shkredov presents a marked improvement to the Korobov bound concerning Zaremba’s conjecture in the theory of continued fractions.

Bounding Zaremba's conjecture

A new bound concerning Zaremba’s conjecture

Special geometries play a key role in string theory and gravitational theories in general. The 6 compact dimensions of the 10-dimensional (super) string are often taken to be a Calabi-Yau manifold. Such compactification is important as it allows us to realise our 4-dimensional spacetime within the theory, and leaves some of the original supersymmetry unbroken. When fluxes are included to describe the analogies of EMFs within the compact space, the supersymmetry condition is modified and defines a new class of manifolds that generalise the notion of a Calabi-Yau space.

In this LonTI series, Prof. Daniel Waldram introduces some formalism and tools useful for characterising such geometries. An outline of purely geometrical backgrounds is given, using general notions of a G-structure and special holonomy. Backgrounds that have non-trivial fluxes are then described. The narrative of the series is guided by applications to string phenomenology and the AdS/CFT correspondence.

## Event info
---
This is a three-part lecture series from LonTI. Lectures are on Mondays at 10:30 am in Tyndall’s Parlour at the London Institute, on the second floor of the Royal Institution, followed by drinks and snacks onsite. To register and attend, please visit [lonti.weebly.com](https://lonti.weebly.com/).

Prof. Daniel Waldram introduces the formalism and tools for characterising geometries in gravitational theories, such as Calabi-Yau manifolds.

Geometry and fluxes

Geometry is so much more than measurements of shapes. It is the heart of physics and mathematics. Inscribed above the door of Plato’s Academy in Athens was “Let no one ignorant of geometry enter!”

In this renowned Friday Evening Discourse, Prof. Yang-Hui He takes us through time and space, from geometry’s classical beginnings to the Renaissance and the Enlightenment, to our current understanding of spacetime itself. In the 19th century Gauss and Riemann considered the relaxation of Euclid’s axioms, resulting in the explosion of post-Euclidean geometry, paving the way for Einstein’s theory of relativity and the birth of modern physics. Singularity solutions of spacetime geometry gives us the discovery of black holes. String theory, attempting to unify quantum mechanics with relativity, delivers a brave new world of quantum geometry. Anyone at risk of ignorance can rest assured, they will soon be fit to enter through Plato’s doors.

This event takes place in the lecture theatre at the Royal Institution. London Institute guests are invited to join the speaker after for drinks and canapés in our private rooms.

At the Royal Institution's Friday Evening Discourse, Prof. Yang-Hui He recounts the creation of modern physics at the hands of geometry.

A revolution in geometry

How geometry created modern physics

Imagination is crucial for creativity and success. In business, where it underpins competitive differentiation and profits, the timescales for reinvention are contracting, while many resources, such as capital, are increasingly scarce. This trend is also reflected in scientific discovery, where the stakes are higher than ever.

In this event, our Trustee Martin Reeves debunks some of the romantic myths surrounding imagination—the idea that it is a solitary enterprise, relying on a eureka moment—and analyses what imagination is and how we may take a systematic approach to harness it, to become powerful “imagination machines”. 

Illustrating his argument, he highlights key examples of businesses that have cultivated imagination, explaining how they secure a competitive advantage. He also delves into the story of the Royal Institution, where transformative discoveries have been made, in this historic imagination powerhouse.

This event takes place in the lecture theatre at the Royal Institution. 


Our Trustee Martin Reeves explores imagination at its core, rethinking previous romantic notions, asking if we can harness it systematically.

The imagination machine

The imagination machine: revisiting creativity

Design is at the interface of function, beauty and order. Throughout history, it has had many points of contact with mathematics, which is the language for describing patterns. These have ranged from the theory of proportion, to symmetry and architecture, to [grid systems and modularity](https://lims.ac.uk/perspectives/designing-web-design/), to simplicity and industrial design, to self-similar fractals and aperiodic tilings, to the dependence of behaviour on the layout of space, to the design of intelligent organisations.

At this meetup, a mix of designers, artists, physicists and mathematicians talk about the present and future of design and mathematics. Four five-minute talks are interspersed throughout the evening to stimulate informal conversation. The purpose of the event is to explore ideas and build connections.

The event takes place at the London Institute for Mathematical Sciences, on the second floor of the Royal Institution in Mayfair. Drinks are provided. If you would like to attend, please email at@lims.ac.uk.

Designers and theorists talk about the intersection of design and mathematics in visualisation, architecture, digital design and industry.

Design meets mathematics

In particle physics, models of interactions between an endless variety of possible particles in any number of spatial dimensions can be constructed, with each situation described by its own quantum field theory. Conformal field theories are a special type of quantum field theory, in that they are scale invariant. They have key applications and provide insights in condensed matter physics, statistical mechanics, quantum statistical mechanics, and string theory.

In this LonTI series, Dr Andreas Stergiou motivates the study of conformal field theory, contextualising the “old” way of studying it as endpoints of renormalisation group flows. The conformal bootstrap method is introduced, which allows for computing formulas that encode relationships between particles described by the conformal field theory. The method exploits conformal symmetries to solve for critical exponents, constraining the correlation functions. Both analytical and numerical implementations are discussed.

## Event info
---
This is a four-part lecture series from LonTI. Lectures are on Mondays at 10:30 am in Tyndall’s Parlour at the London Institute, on the second floor of the Royal Institution, followed by drinks and snacks onsite. To register and attend, please visit [lonti.weebly.com](https://lonti.weebly.com/).

Dr Andreas Stergiou delivers an introduction to the conformal bootstrap method which is used to constrain and solve conformal field theories.

Conformal bootstrap

Conformal field theories and conformal bootstrap

We are delighted to host the London Algebra Colloquium for their final seminar of 2022. For over seventy years, algebraists from across London and beyond have met regularly at this colloquium to discuss research and ideas in this sphere of pure mathematics. 

In this talk, Frank Neumann presents the Hochschild cohomology of differential graded categories. This is a homology theory that admits the characteristic homomorphism, a natural map to the graded centre of its derived category. When interpreted as an edge homomorphism in a spectral sequence, this map can be studied systematically, enabling its application to examples in algebra, geometry, topology and physics. The framework can be extended beyond DG-categories to A-infinity-categories.

As a festive treat and at the invitation of London Institute Fellow Prof. Yang-Hui He, a regular attendee of LAC, this meeting will be held in Tyndall’s Parlour at the London Institute, on the second floor of the Royal Institution.

Previous talks given by the London Algebra Colloquium and further details about the society can be found on their [website](https://londonalgebra.wordpress.com). 



The London Institute hosts guest speaker Dr Frank Neumann and the London Algebra Colloquium for their final seminar of 2022.

Cohomology and sequences 

Hochschild cohomology and spectral sequences

In February, Prof. Maryna Viazovska won the Fields Medal for her work on sphere-packing formulas. She is only the second woman to receive the award, which is the most acclaimed in mathematics, in its 86-year history.

In this event, Prof. Viazovska will speak with London Institute Fellow and BMUCO advisor Prof. Yang-Hui He about her proof that the E8 lattice provides the densest packing of identical spheres in eight dimensions, her contributions to related external problems, and her efforts with interpolation problems in Fourier analysis. She will also touch on her efforts with geometric optimisation problems and her championing of academic freedom in light of the war in Ukraine, where she was born and many of her relatives remain. 

For the conversation and Q & A session, which Prof. Viazovska will attend by live-stream, participants are invited to join digitally or in person in the London Institute’s Tyndall’s Parlour on the second floor of the Royal Institution. In either case they must complete this [form](https://docs.google.com/forms/d/e/1FAIpQLSeA2KpKOo1pRwwtDE3iQsPMV6sZGgFgttd7BPqT6bx90atymA/viewform). This event is organised by the science NGO, [BMUCO](https://www.bmuco.org), in partnership with the London Institute.

The Ukrainian mathematician Prof. Maryna Viazovska, who won this year’s Fields Medal, joins us for a virtual interview and discussion.

Spheres of influence

In conversation with Prof. Maryna Viazovska

In terms of quantum field theory, this is another example of the duality between a fluctuating vector field and fluctuating geometry. He will present new exact solutions of Navier-Stokes and Euler equations and investigate in detail the loop equation suggested in the early 1990s. The loop equation plays the same role in the theory as the Boltzmann kinetic equation in statistical physics. It has the form of the Schrödinger equation with a complex Hamiltonian in loop space. The viscosity plays the role of Planck's constant. Strong turbulence corresponds to the WKB limit of the loop equation.

In this limit, he finds a fixed point of the loop equation he calls Kelvinon. Kelvinon has a conserved circulation for a fixed loop in space, generalising Kelvin's theorem. The Clebsch field of this solution has a nontrivial topology with two winding numbers. These topological conservation laws allow us to compute the PDF of circulation in a WKB limit (large circulation in the viscosity units). This PDF perfectly matches the results of numerical simulations of the conventional forced Navier-Stokes equation.

## Programme

Mon 5 Dec 2022

- *10:00* Lecture 1
- *12:00* Lecture 2 

- Wed 7 Dec 2022

- *10:00* Lecture 3
- *12:00* Lecture 4
- *1:00* Q&A

Over the course of four lectures, Prof. Alexander Migdal will present 35 years of research concerning his new approach to strong turbulence.

Strong turbulence

Speaker

Quantum theory of classical turbulence

### Theoretical life

The London Institute’s “Theoretical life” series tackles basic science questions about life itself, of which biology is just one instance. It is done in conjunction with bit.bio, with whom we work to decode the operating system of life. Topics range from the structure of genetic computation, to the thermodynamics of emergent self-replication, to cell programming and out-of-equilibrium switching, to a mathematical theory of programmed ageing, to learning and high-dimensional inference.

After each talk, there is a high-level panel discussion, followed by drinks and discussion on site.

### Evolution and Occam

Why does evolution favour symmetric structures when they only represent a minute subset of all possible forms? Just as monkeys randomly typing into a computer language will preferentially produce outputs that can be generated by shorter algorithms, so the coding theorem from algorithmic information theory predicts that random mutations, when decoded by the process of development, preferentially produce phenotypes with shorter algorithmic descriptions. Since symmetric structures need less information to encode, they are much more likely to appear as potential variation. Combined with an arrival-of-the-frequent population genetics mechanism, this evolutionary Occam’s razor predicts a much higher prevalence of low-complexity (high-symmetry) phenotypes than follows from natural selection alone. It explains striking patterns observed in protein complexes, RNA secondary structures, a gene regulatory network and Richard Dawkins’ biomorphs model of development.

### Finding transcription factors for cellular reprogramming

Cellular reprogramming is erasing a specific cellular identity from a population of cells and establishing another, such as turning skin cells to muscle cells. Transcription factor overexpression is the most efficient and robust method to exchange cellular identity.

Transcription factors are proteins that bind to specific gene regulatory elements in the genome and control gene expression. I will talk about experimental and predictive methods to identify transcription factors that can install specific cellular identities, for generation of human cell types for biomedical research and cell-based therapies.



The algorithmic nature of evolution implies an exponential bias towards simpler phenotypes, explaining an observed preference for symmetry.

Evolution and Occam’s Razor

Does evolution have an inbuilt Occam’s Razor?

The pioneering work of Bekenstein and Hawking in the 1970s showed that black holes have thermodynamic properties like temperature and entropy, just like the air in a room. This leads to the question: can we account for the thermodynamic entropy of a black hole as a statistical entropy of an ensemble of microscopic states? One of the big successes of string theory is to answer this question in the affirmative for a large class of black holes. The aim of these lectures is to introduce these ideas to early researchers in high energy physics and mathematical physics.

This four-part series by ​​Prof. Sameer Murthy provides an orientation and the basic ideas and techniques used in black hole microstate counting. The lectures will cover the following topics in succession: the thermodynamics of black holes; the entropy of black holes in string theory; a special class of black holes called BPS black holes; and an illustration of some actual calculations of entropy. They take place over four weeks in Tyndall’s Parlour at the London Institute for Mathematical Sciences, on the second floor of the Royal Institution.

## Black hole mechanics

Lecture 1 reviews the basics of black hole thermodynamics, including the four laws of black hole mechanics, analogous to the usual four laws.

## Black hole entropy

Lecture 2 describes the ideas underlying the counting of the statistical entropy of black holes in string theory, and implications for it.

## BPS black holes

Lecture 3 covers a special class of black holes for which the entropy can be calculated and the corresponding microscopic ensemble of states.

## Don’t drink and derive

Lecture 4 shows how to actually calculate the statistical entropy in practice, in particular for some simple examples of BPS black holes.



Prof. Sameer Murthy talks about the thermodynamic entropy of a black hole and how to formulate it within a statistical physics foundation.

Black hole microstate counting

Introduction to black hole microstate counting

A swirling quasi-particle, a knot of twisting field lines, or a subatomic hurricane? Skyrmions aren’t easy to describe in words, yet that’s the challenge Prof. Nicholas Manton tackles in his new book, Skyrmions: A Theory of Nuclei.

In this event, Prof. Manton takes us through the  60-year history of Skyrme theory, which was first proposed in 1962 by British physicist Tony Skyrme as a way of modelling subatomic entities like protons and neutrons using convoluted twists in the quantum pion field. It was later superseded by quantum chromo-dynamics and its quarks, but, more recently, Skyrmions have been revived by researchers working on the structure of atomic nuclei, because quantum chromo-dynamics is extremely hard to solve. ​In his book, Prof. Manton touches on some of the variants of Skyrme theory—which incorporate mesons heavier than pions, and extend the theory to include particles such as kaons—before introducing the Sakai-Sugimoto model, which relates Skyrmions to gauge theory. A different type of Skyrmion describes magnetic fields that can be coaxed into forming vortex-like swirls in some special materials.

Afterwards there will be a discussion. Then we will celebrate the launch of Prof. Manton’s book, which is replete with beautiful colour illustrations.

## Programme

- *14:00* Seminar on skyrmions by Prof. Nicholas Manton
- *15:00* Discussion and book launch

Prof. Nicholas Manton will talk about the 60-year history of Skyrme theory, as he launches his new book on the subject.

Skyrme theory at 60

Quantum field theory is typically not solvable in closed form and represents a complex and accurate description of elementary particle physics. Integrable quantum field theories, while sufficiently simplified, still exhibit a rich range of effects. They normally reside in a 1+1 D world, and are characterised by exact S-matrices which are calculable in closed form from fundamental physical requirements such as unitarity, crossing symmetry and the location of bound states. Thanks to their vast symmetry, such models are an ideal playground for understanding non-perturbative quantisation. The theory of integrable systems also plays a role in recent advances in string theory.

In this LonTI series, Prof. Alessandro Torrielli describes the duality between two integrable systems: the 2D Sine-Gordon model and the 2D Thirring model. He outlines the classical and quantum Sine-Gordon models, in particular the spectrum, S-matrices and underlying quantum symmetry. He then presents the duality with the Thirring model. Prerequisite knowledge is kept to a minimum, and lecture notes with exercises are available online.

## Classical Sine Gordon

Lecture 1 gives an introduction to classical and quantum integrability, and describes the Sine-Gordon model and its soliton solutions.

## Quantum Sine-Gordon

Lecture 2 sets out quantisation of the classical picture, and algebraic aspects of quantum Sine-Gordon, such as relations with spin-chains.

## Sine-Gordon and Thirring duality

Lecture 3 describes the duality between the Sine-Gordon model and the Thirring model and provides a particular test using form factors.

Prof. Alessandro Torrielli talks about integrable quantum field theories and the duality between the 2D Sine-Gordon and 2D Thirring models.

Sine-Gordon/Thirring duality

Sine-Gordon and Thirring model duality

Good conjectures can inspire new branches of mathematics and theoretical physics. They usually come from spotting patterns and applying instinct. Because in mathematics there are no coincidences, automated pattern detection is immune to the false positives that plague experimental science. Can machines help us make mathematical discoveries and speed up theoretical research? 

There has been a recent surge of interest in using machine intelligence to study various aspects of geometry, topology and representation theory. Theoretical physics has helped drive these developments, through the percolation of ideas and analogies and by providing an effective testbed for learning methods. One pertinent example is machine-driven studies of the algebraic geometry of Calabi—Yau spaces, which appear as extra-dimensions in string theory.

In this one-day symposium, we discuss how to assist and automate new mathematical discovery by exploiting novel computation and deep learning, as well as insights into the theory of learning itself. At 4pm there is a high-level panel discussion for a broader audience on the future of AI-assisted discovery, and the roles of academia versus industry. This is followed by drinks and dinner on site.

## A two-way street

Several of the success stories in AI-assisted mathematics have relied on the deep learning architectures of neural networks and their remarkable ability to act as universal function approximators. Well-known feature attribution techniques recently led to exciting new results in knot theory and representation theory. Even number theory, normally resistant to such approximations, is now proving susceptible to certain forms of learning.

But the reverse is also true: mathematics is shedding light on deep learning. As we develop better theories of learning, profound connections to well-studied areas of mathematics are becoming apparent. The Kolmogorov-Arnold representation theorem seems structurally similar to neural networks, with deep connections to Hilbert’s 13th problem. More recently, researchers established that training in neural networks, when viewed geometrically, is a variant of Ricci flow. Using such links to leverage modern machine learning algorithms will lead to surprising breakthroughs in mathematics and physics, as well as a better understanding of machine learning itself.

## Programme

Old Post Room
- *10:00* Coffee, meet and greet 

- Tyndall Parlour
- *10:20* LIMS, AI and mathematics: Thomas Fink 
- *10:30* Opening remarks: Challenger Mishra

- *10:40* Knot theory and machine learning: Andraz Juhasz
- *11:00* Machine learning with mathematicians: Alex Davies
- *11:20* Teaching theorems to computers: Kevin Buzzard

- Old Post Room
- *11:40* Coffee and discussion

- Tyndall Parlour
- *12:00* Machine-Learning Mathematical Structures: Yang-Hui He
- *12:20* Towards a human-like reasoning system: Mateja Jamnik
- *12:40* Draft, sketch and prove: Wenda Li

- *13:00* Local pub lunch and sandwiches on site in Bragg’s Dining Room

- Tyndall Parlour
- *14:00* Peter Braam 
- *14:20* Syllogistic reasoning and beyond: Tiansi Dong

- Old Post Room
- *14:40* Coffee and discussion

- Bragg’s Dining Room 
- *15:00* Speed dating: AI vs mathematics
 
- *16:00* Break

- Tyndall Parlour
- *16:15* High-level panel discussion with business leaders and journalists

- *17:45* Drinks in the Old Post Room
- *19:00* Dinner in Faraday’s Study


## Talks

To encourage understanding and discussion, talks are 20 minutes long and can have at most three slides. A blackboard is available to explain ideas and results.

## Venue

We will meet in the Tyndall Parlour of the London Institute, which is on the second floor of the Royal Institution.

## Financial support

This symposium is funded by the Henderson Institute at the Boston Consulting Group. For those outside of London, we can cover travel to London and overnight accommodation. Additional sponsorship comes from the Accelerate Program for Scientific Discovery at The Computer Laboratory, Cambridge. 

<a href="https://docs.google.com/forms/d/e/1FAIpQLSc6CFfd723x6gRK2Ec-Q4lMlKjX7h76OisthWhNOEdgB6ZMPg/viewform?usp=sf_link">Register</a>

The London Institute hosts a day symposium on using AI to speed up mathematical discovery, followed by a panel discussion, drinks and dinner.

AI mathematics

Speakers and panel members

AI-assisted mathematical discovery

The equations governing scalar field theory and electromagnetism are well posed. When it comes to gravity, by contrast, there are aspects that remain unresolved—in particular, the role of timelike boundaries. Yet that investigation goes to the heart of general relativity and is playing an increasingly important part in studies of, for instance, the TTbar deformation in the AdS/CFT correspondence, and aspects of holography in de Sitter spacetimes. Numerical studies point towards the existence of instabilities, and recently, rigorous theorems have been proven regarding the nature of the initial boundary value problem in gravity with timelike boundaries. 

The aim of this workshop it to bring together experts on mathematical, numerical, and holographic aspects of timelike boundaries in gravity, with the aim of connecting the mathematical and physics literature and in the process creating a common language for future research.  

The event is hosted by the London Institute for Mathematical Sciences, which is based at the Royal Institution. It will take place in the Faraday Room on the second floor. 

## Programme

- *10:00 - 11:15* Ted Jacobson (U. of Maryland)
- *11:15 - 11:45* Coffee Break 
- *11:45 - 13:00* Jacques Smulevici (Sorbonne U.)
- *13:00 - 14:30* Lunch Break
- *14:30 - 15:15* Vasudev Shyam (Stanford U.)
- *15:15 - 15:30* Short Break
- *15:30 - 17:00* Discussion session led by Eleanor Harris (KCL) and Andrew Svesko (UCL)
- *17:00* Drinks at the London Institute

The London Institution hosts a one-day workshop exploring the role of timelike boundaries in the context of gravity, followed by drinks.

Boundaries in gravity

Timelike boundaries in gravity

This month, a little over 400 years ago, the Mayflower pilgrims set sail from England’s south coast and crossed the Atlantic, making landfall in Massachusetts about fifty miles from the present-day location of MIT. On 6 September, we are bringing the US and the UK together again to celebrate MIT as a powerhouse in physics, and the London Institute as the new theoretical science tenant at the Royal Institution. 

This event is timed to coincide with Prof. Peter Fisher’s departure as Head of Physics at MIT. We will watch his live-streamed Royal Institution talk—What is dark matter?—in which he will explain where we are in our quest to understand the true nature of dark matter and what the consequences of this understanding might be. Before and after, past and present members of MIT and the London Institute will discuss this, and lighter matters, over drinks in what was once Michael Faraday’s dining room.

Proceedings will be hosted by the Director of the London Institute, Dr Thomas Fink, and Prof. Yang-Hui He, Fellow of the London Institute and an MIT alumnus. The drinks begin at 6.30pm, the talk at 7pm.

The London Institute welcomes MIT alumni to the Royal Institution to mark Prof. Peter Fisher’s departure as Head of Physics at MIT.

Cheers, Brits and Yanks

Technological innovation improves lives, drives the economy and increasingly shapes international relations. Yet we have little understanding of what drives innovation, why it varies across sectors and states, and how to speed it up through interventions. The London Institute and the Ditchley Foundation are working together to advance [the science](https://lims.ac.uk/project/mathematical-structure-of-innovation/) and implementation of technological change, in ways that don’t destabilise delicately balanced ecosystems. 

At this event, leaders from science, industry and politics will discuss three aspects of technological innovation. The first discussion is on the science of innovation: what it is, how we can predict it, and the extent to which we can speed it up. The second discussion is on the funding of innovation: how can we accelerate the process of knowledge creation, and the translation of ideas into products? The third discussion is on the politics, ethics and culture of innovation: what are the barriers, and which ones can be safely lowered? This event will take place in our rooms at the Royal Institution. After the discussions, there will be informal drinks.

The London Institute and the Ditchley Foundation host an afternoon discussion and drinks on the science of innovation and how to speed it up.

Accelerating innovation

Accelerating innovation: the science, funding and politics

Artificial intelligence can beat humans at poker, chess and Go. It is used to translate languages, sort astronomical images and predict proteins. Some proponents believe that AI will be able to make creative contributions, such as new mathematical conjectures and even proofs of theorems. On the other hand, many believe that AI has not lived up to its promise. Far from approaching artificial general intelligence, AI has not progressed beyond high-dimensional curve-fitting. Deep learning algorithms are globally wired, making them difficult to build up in an engineerable way, as well as hard for humans to understand.

In this talk Prof. Peter Cochrane argues that much of the contention surrounding AI stems from the lack of clear definitions of what intelligence is. Surprisingly, it was the defence industry that triggered rigorous mathematical descriptors of AI performance.  A key step was abandoning comparisons between machine intelligence and biological intelligence, particularly that of humans. With an engineers eye for workable solutions, Prof. Cochrane gives an account of what AI is and where it could go.

Peter Cochrane talks about how quantifying machine intelligence, distinct from biological intelligence, can quell the debate on AI’s future.

Quantifying AI

Quantifying machine intelligence mathematically

Biological life is a self-replicating and self-improving machine. This is the holy grail of technology—a feat that man-made technology is nowhere near achieving. We can give a description of how life works, but we are unable to predictably engineer it to suit our purposes. This is about to change. The ability to read, write and execute the genetic code of cells is transforming biology from a descriptive science to a predictive one.

In this event, cell biologist and bit.bio founder Mark Kotter explains how breakthroughs in programming cells are kicking off a revolution. Here, a handful of genes causes one kind of cell, such as muscle, to transform into another, such as neurons. This big effect from a small cause is the result of genetic subroutines, functional modules that can be recombined. Think of these like the subroutines in digital software, with a twist: biological software can influence the very hardware on which it runs. Working with mathematicians at the London Institute, bit.bio is uncovering the operating system of life, setting the stage for a biological analogue of the silicon revolution.

Breakthroughs in cell programming are kicking off a biological analogue of the silicon revolution, allowing us to predictably engineer life.

Uncovering the OS of life

The cell programming revolution

Achieving external control of cell programmes can allow for the fine manipulation over cell identity, with the potential to reverse damage and treat diseases. Despite isolated experimental successes, mathematical models for understanding cell identity and predicting cell transitions remain elusive. This is partly due to the complexity of cell regulation, which involves processes across multiple time and organisational scales. It also stems from a disconnect between the research culture of cell biologists and mathematical scientists. We urgently need theoretical models to catch up with experimental observations so that we can make this qualitative field more predictive.

This intimate two-day meeting, hosted by the London Institute and the Cambridge cell-coding company bit.bio, is a call to arms, bringing together researchers from physics, mathematics, machine learning and cell biology. It emphasises spirited discussions over scientific presentations. It takes place in the historic Lecture Theatre at the Royal Institution used by Davy and Faraday, with break-out sessions in the adjoining heritage rooms.

## Programme

The workshop will include 9 talks across the 3 themes of biology, theory and computation aimed at giving a broad perspective on the challenges and open questions in cell programming. Between these, attendees can participate in chalk talks given at blackboards placed throughout the RI’s library and anteroom. These are an opportunity for smaller and more interactive discussions where participants can present recent advances they have made, problems they face in research and work collaboratively towards new approaches.

### Wed 9 Mar 2022

- *19:00* Informal welcome dinner off site, location TBC

### Thu 10 Mar 2022

- *09:00* Early Arrivals 
- *09:15* Tea, coffee, pastries
- *10:00* Welcoming, Overview of day 1
- *10:30* Talk 1: Mark Kotter
- *11:00* Talk 2: Jasmin Fisher
- *11:30* Coffee break
- *12:00* Talk 3: James Briscoe
- *12:30* Talk 4: David Rand
- *13:00* Buffet Lunch in the Ante Room
- *14:00* Chalk Talks Session 1
- *15:00* Chalk Talks Session 2
- *19:00* Public talk in the Royal Institution Lecture Theatre
- *20:00* Dinner Reception

### Fri 11 Mar 2022

- *09:00* Early Arrivals 
- *09:15* Tea, coffee, pastries
- *10:00* Welcoming, Overview of day 2
- *10:30* Talk 1: Benedikt Berninger
- *11:00* Talk 2: Antonio del Sol Mesa
- *11:30* Coffee break
- *12:00* Talk 3: Ben MacArthur
- *12:30* Talk 4: Ana Martin-Villalba
- *13:00* Buffet Lunch in the Ante Room
- *14:00* Chalk Talks Session 1
- *15:00* Chalk Talks Session 2

## Chalk Talks

What is valuable about an in-person workshop? Chalk talks are an attempt to step back from the usual technical seminar, towards a more interactive and collaborative way of communicating. In a chalk talk, one researcher leads a small group discussion at the blackboard for 30 to 45 minutes. The format is flexible—it can be anything from a high level overview of results to a panel discussion on a topic that needs rethinking. Chalk talks are a chance to leverage the tremendous expertise we have gathered and to form long-term connections and collaborations. Think of them as an extension of a group meeting to the wider cell programming community.

To propose a chalk talk, please submit a short summary of the discussion below. We will do our best to fit it in and keep a balance across the themes of the workshop. Be creative. As this is an experiment, it relies on a willingness to try new things out.

The London Institute and bit.bio host a two-day international meeting to unravel the theory of cell programming at the Royal Institution.

Cell programming maths

Meeting of minds on the mathematics of cell programming

Academic seminars tend to be one-off events that focus on the latest research of the speaker. But when it comes to learning about a field of research, seminars are ineffectual. To fill this gap in the market, a group of graduate students in theoretical physics formed the [London Theory Institute](https://lonti.weebly.com/), or LonTI. It organises series of lectures in exciting areas of theoretical physics, open to all young researchers. The difference between seminars and LonTI talks is like the difference between traditional episodic TV shows, and recent sequential TV series that provide a slower but more satisfying experience.

At each weekly talk, there is a lecture by a specialist, followed by discussion over lunch on site. The meetings take place at the London Institute, on the second floor of the Royal Institution. Topics range from observables in gauge theories, to spin chains in AdS/CFT, to gravity and black holes in AdS. LonTI provides an opportunity to meet like-minded theorists, cutting across universities and subfields. It is supported by the Science and Technology Facilities Council and the London Institute.

During spring, the London Institute hosts weekly lectures in theoretical physics for young researchers who are interested in new fields.

LonTI lecture series

LonTI lecture series in theoretical physics

Since time immemorial, mankind has responded to stories. Recently, anthropologists and scientists—from Joseph Campbell to Randy Olsen—have tasked themselves with exploring the fundamental structures of stories, uncovering story types and patterns that repeat across the centuries. Film-makers and novelists have used these to tremendous effect, harnessing the power of the hero's journey to create unforgettable narratives. Yet scientists, by contrast, have been slow on the uptake.

In this event, Prof. Alison Woollard talks about the science of storytelling and storytelling in science. A Royal Institution Trustee who gave the iconic Christmas Lectures, she touches on the neuroscience of learning, the role of story in primitive cultures and the structure of story. Moreover, she argues that story is a crucial ingredient in communicating scientific discovery, which we hold as a core belief at the London Institute.

The event is in our 2nd-floor seminar room in the Royal Institution. After introductory drinks at 5:00, the talk starts at 5.30, followed by drinks and discussion afterwards. RSVP at smc@lims.ac.uk.

Prof. Alison Woollard explores the science of storytelling and storytelling in science—a neglected virtue in modern scientific research.

The science of storytelling

To many people, the phrase “the theory of everything” conjures memories of the Oscar-winning film about the life and science of Prof. Stephen Hawking. Yet the quest referred to in that title goes back much further. It is nothing less than the search for the holy grail of science: an elegant unified theory, encompassing all matter, forces and space-time itself. It stretches from Galileo and Newton, via Einstein and Dirac, to the most recent advances in superstring theory.

In this event, Prof. Yang-Hui He presents the story as a dance of discovery between data, physics and mathematics, each anticipating the other’s moves. They have all taken the lead at different times, yet for many today, including Prof. He, the guiding principle is the rigour and beauty of mathematics. It is fitting that this event is held at the Royal Institution, where Faraday uncovered the principles of electromagnetism. These inspired Maxwell's equations, a key component of any unifying theory.

<a href="https://youtu.be/llGvkEgXnAQ">Watch the event</a>

Professor Yang-Hui He tells the captivating story of the holy grail of science: the mathematical quest for a unifying theory of everything.

The Theory of Everything

Sir Roger Penrose is a mathematical physicist with the eye of an artist and the soul of a philosopher. He won the 2020 Nobel Prize in Physics for his work on the mathematical foundations of black holes. The tilings which bear his name can cover the plane in a never-repeating pattern. His work on the theory of mind suggests consciousness is a peculiarly human capability. He is a master word-smither, capable of rendering the most complex ideas clear, and his popular books have inspired a generation of physicists and laymen alike. 

In this event, Sir Roger joins Dr Thomas Fink and Prof. Yang-Hui He on stage for a conversation about the man behind the science. We take a rare look into the workings of this singular mind. How does he get his ideas? Is beauty a guide to truth? What’s the basis of free will? Is AI a threat? Can art inform science? Is man different from machine? Do universities monopolise research? The discussion takes place in the Faraday lecture theatre at the Royal Institution. Afterwards, guests are invited to join the speakers for drinks and canapés in the London Institute’s private rooms.

<a href="https://youtu.be/sYRti8ZU5s8">Watch the event</a>

Sir Roger Penrose talks about physics, philosophy and art in a conversation with Thomas Fink and Yang-Hui He in the Faraday lecture theatre.

Talking to Penrose

In conversation with  Sir Roger Penrose

Are machines intelligent? Far from approaching artificial general intelligence, AI seems not to have progressed beyond high-dimensional curve-fitting. But hiding in plain sight is perhaps the most compelling of all AI achievements: Mathematica, a general system for solving mathematical equations and manipulating mathematical expressions. Mathematica has developed as well into a functional programming language and the leading platform for visualising mathematics and data.

In this event, Conrad Wolfram tells the story of how he and his brother Stephen Wolfram transformed the way that scientists do mathematics. As well as giving an inside account of the past, Mr Wolfram also peers into the future. Can we use machines to help identify new mathematical conjectures and speed up theoretical research? Is computational thinking at the heart of scientific research, and even how we understand and teach mathematics? This seminar takes place in what used to be Michael Faraday’s private apartment, marking the launch of the London Institute’s seminar series in its new home at the Royal Institution in Mayfair.

Conrad Wolfram describes how two brothers harnessed machines to do mathematics, changing the way we think about computational thinking.

Mathematics & machines

Michael Faraday was born on this day 230 years ago. While Princeton University was celebrating its 45th anniversary, it would be 100 years before the founding of the California Institute of Technology. Despite the age gap, both U.S. universities would go on to become powerhouses in physics. To celebrate the birthday of Faraday, one of the founding fathers of physics, Princeton and Caltech alumni meet at the London Institute in the Royal Institution, where Faraday worked.

At this event, which takes place in what was once Faraday's private apartment, past and present members of Princeton, Caltech and the London Institute get to know each other over drinks. Dr Thomas Fink gives a brief account of how the London Institute got started. Then Prof. Yang-Hui He gives a short tour of fundamental physics, pure mathematics and machine learning. From Newton to Faraday to Einstein to recent advances in superstring theory, our understanding of the universe is threaded by mathematical beauty. Prof. He shows how physics, mathematics and AI constitute an entangled trio that dance a steady Sarabande through history.

Princeton and Caltech alumni celebrate Faraday’s birthday at the London Institute for Mathematical Sciences, inside the Royal Institution.

Cheers to Brits and Yanks

Writing about the The Three Princes of Serendip, Horace Walpole records that the princes “were always making discoveries, by accidents and sagacity, of things they were not in quest of”. Serendipity is the fortunate development of events, and many organizations stress its importance. Researchers at the London Institute recently showed that [serendipity has a mathematical foundation](https://lims.ac.uk/paper/serendipity-and-strategy-in-rapid-innovation/). This is just one example of the research that we do on the [theory of human enterprise](https://lims.ac.uk/projects/theory-of-human-enterprise/). Other projects include markets and the mind, cascading risk in finance, repairable instead of robust, the future of technological progress, and the mathematical structure of innovation.

At this event, we are creating opportunities for serendipity by bringing together leaders in business, finance and physics at the London Institute for Mathematical Sciences, a private institute for curiosity-driven research based at the Royal Institution in Mayfair. We meet in Michael Faraday’s former private apartment, where an informal lunch is provided. The aim of this event is to get to know each other—and discover things we are not in quest of.

The London Institute is hosting a lunch at the Royal Institution to promote serendipity between leaders in business, finance and physics.

In search of serendipity

Serendipity in business, finance and physics

The Chern Institute is a premiere research centre for mathematics. It is named after Prof. Shiing-Shen Chern, one of the greatest mathematicians of the 20th century, and an alumnus of Nankai University. A strong proponent for dialogues between mathematics and theoretical physics, Prof. Chern had hoped for a regular international symposium in this subject. When he died in 2004, he wished his ashes to be buried in front of the institute so that “I can hear future dialogues in mathematics,” he said.

At this [symposium](https://sites.google.com/view/cim-dialogues/), 80 speakers from various disciplines in pure and applied maths will give colloquium-style talks aimed at a general mathematics audience over two weeks. The goal is to encourage mathematical dialogues across subfields. Since joining Nankai as a visiting Chair, the London Institute’s Prof. Yang-Hui He has been organising this symposium with Profs. Mo-Lin Ge and Cheng-Ming Bai, both directors of the Chern Institute. This year it will be held online. To mark the 110th anniversary of Prof. Chern’s birth, Sir Roger Penrose will deliver the public lecture, on the occasion of his own 90th birthday.

Yang-Hui He co-organises the Nankai Symposium on dialogues between mathematics and physics, with the plenary talk by Sir Roger Penrose.

Mathematical Dialogues

‘We are capable of so much more than we could ever imagine’, said rock climber Tommy Caldwell in the movie Dawn Wall. His story is about physical achievement. But his idea also applies to creative work—whether it’s proving a theorem, writing a paper or planning a research grant. What is the limit of human achievement, and how can we get closer to it? 

To find out, we did an experiment to test what happens when we separate ourselves from daily distractions to work exclusively on a single problem. We sent a small team to a Greek island for a week to write a research grant proposal. The trio stayed at a remote villa, with only the project and the sea to occupy them. By the week’s end, they cracked the proposal. Here is what they noticed along the way.

First, travelling to a remote place reduces our emotional concern with life back home, so sustained focus is a lot easier. Second, when a team is constantly immersed in the same problem—breakfast, lunch and dinner—the opportunities for superadditivity skyrocket. Third, progress starts slow but accelerates quickly, which is why a trip of at least a week is key.

What is the limit to human achievement? To find out, we sent a team to a Greek island for a week to immerse themselves in a single problem.

Greek week

While working at Bell Labs, information theory pioneer Richard Hamming asked his colleagues to name the most important problems in their fields. Later, he asked them what they were actually working on. To his surprise, the two sets of answers didn’t overlap. Yet as he pointed out, “If you don’t work on important problems, it’s unlikely you’ll do important work.” To encourage scientists to work on the biggest challenges, Britain has launched the Advanced Research and Invention Agency. Its aim is to support work on radical new theories and technologies that don’t just solve the pressing problems of our time, but bypass them altogether. 

To mark the launch of ARIA, researchers at the London Institute meet for a one-day symposium to figure out the most important mathematical challenges of our time. Inspired by David Hilbert’s influential list of problems from 1900, the number of challenges is limited to 23. As well as a potential road map for ARIA, our list is a reminder to the scientific community to aim high. The symposium takes place on the birthday of the founder of the Royal Institution, Lord Rumsford.

A one-day symposium of physicists and mathematicians to write down a list of the 23 most important mathematical challenges of our time.

23 mathematical challenges

String theory—with its cornerstones of supersymmetry and extra space-time dimensions—has been a muse to pure mathematics. The discipline has provided novel methods of attack for a myriad of mathematical problems: from enumerative geometry to Moonshine, from quantum invariants to mock modular forms. Central to string theory is the study of Calabi-Yau manifolds, which serve as a beacon to such important investigations as compactification, mirror symmetry, moduli space and duality.

In this talk, Yang-Hui reviews how the problem of string phenomenology led physics first to algebraic and differential geometry, then to computational geometry, and now to data science and AI. How did this pencil-and-paper driven field become increasingly suited to computational techniques? Within the playground of the Calabi-Yau landscape, accumulated over four decades by physicists, mathematicians and computer scientists, He shows how the latest techniques in machine-learning can help explore problems of physical and mathematical interest. This talk is a taster of his book The Calabi-Yau Landscape: from Geometry, to Physics, to Machine-Learning.

In this in-real-life only event, Yang Hui talks about how string phenomenology has led from differential geometry to computational geometry and now to machine learning.


Superstrings, Calabi-Yau manifolds and machine learning

The London Institute's Christmas party was a case of swine before pearls. Postdoc Alexander Mozeika provided the swine, in the form of a small pig from his Camden butcher, which was roasted in the fireplace. The pearls came later, courtesy of Institute alumnae Antonia Tingey and Bethia Beadman, supported by office manager Victoria Harrison. Lobbyist Vernon Hunte from the PR firm April Six got in the spirit of things with a dose of his stand-up comedy. The offspring of a Trinidadian and an Italian, Vernon calls himself a "pasta-farian".

Late in the evening, research associate Robert Bywater expressed his approval by gnawing on a trotter. Meanwhile, graphic designer Daniel Eris proclaimed that the world is swamped with mediocrity—apart from the beast and booze, which were both excellent. Beer and wine flowed freely, but the whisky proved elusive. It was kept in a Klein bottle decanter, a three-dimensional object with no interior. A Klein bottle can be constructed at home by gluing together two Möbius strips along their edges. In the party invitation, it was drawn entirely mathematically by Robert Farr.

The London Institute marks the year’s successes at its Yuletide Winterfest, from 4pm on Friday 11 December—if it can get the spirits out.

Yuletide Winterfest

Biological systems are incredibly complex, involving interactions across multiple time and length scales. Gene regulation alone involves many molecular species playing specific roles, structural changes in the epigenome and intercellular forces and signalling, all within the chaotic and noisy cellular environment. Despite this complexity, gene regulation gives rise to multicellular organisms where each cell type is robust to genetic diversity and mutations. The genetic code, logic and computation within the cell is, therefore, something we could learn a great detail from. Understanding these processes would not only pave a way for the design of more efficient therapies and revolutionise personal medicine, but enable the development of biological machines.

To make ground towards these end goals we must develop the field of biology, which has traditionally been based on observation, into a predictive science like physics and mathematics. How do we do this? Do we utilize the explosion of big data and the omics revolution to draw inference on experimental results? Or is a ground-up mathematical approach needed to create models that capture the necessary amount of detail without over complicating or simplifying the situation? Likely, it will need a combination of the two techniques. 

Many of the modelling tools we have at our disposal may not currently be up to scratch though. The toolbox of mathematics and physics was largely developed for systems in equilibrium. Thus, these tools often fail in the messy world of biology. This event aims to bring scientists together to discuss promising and novel techniques for modelling cell biology.


We’re bringing mathematicians and biologists together to discuss novel techniques for modelling cell biology on Wednesday, 16th September.

Mathematics of biological computation and logic

Until recently, the idea that developmental biology was a one-way process was widely accepted. The advent of cell reprogramming tore this apart, revealing that cells can retain the ability to change identity. Given the complexity of genetic and cellular processes across multiple organizational length scales, the mechanisms driving cell fate are still obscure. Following our recent <a href="https://lims.ac.uk/perspectives/decoding-cell-programming/ ">partnership with Bit.Bio</a>, we are building theoretical models and methods of inference to shed a light on the programmes piloting cellular function. We’re also recruiting theorists in cell programming and machine learning.

In this event, we investigate theoretical approaches to describe and predict cell identity, shaped by experimental innovations at Bit.Bio. Applied mathematician and LIMS postdoc Ryan Hannam talks about building models of gene regulation and cell identity grounded in biological fact. Cell coding company Bit.Bio discusses their breakthrough technology, followed by another speaker we are recruiting; if you want to talk, email Ryan at rh@lims.ac.uk. After, there is general discussion on how to accelerate this moonshot mission.

Staying safe at LIMS during COVID-19

The London Institute has taken all necessary actions to ensure it complies with the government’s guidance on managing the risk of COVID-19 at the workplace. We are fortunate to have a building with sufficient space to keep people appropriately separated. If you have questions, please contact Ben Lynch at bl@lims.ac.uk.

Physicists and biologists discuss theoretical models of cell programming and reprogramming, shaped by experimental innovations at Bit Bio.

Reprogramming the cell

How useful is mathematical modelling in biology? Given the complexity of genetic and cellular processes across multiple organizational length scales, biology has eluded a rounded description in terms of a handful of fundamental equations. But there is compelling evidence that this intricacy masks elegant underlying structure: the nominal information content of (coding) DNA, the plasticity of early cell identity, and the adaptive immune system.

In this event, we investigate the state-of-the-art for using our ever-increasing mathematical toolbox to describe and predict biological processes with comparatively simple models. Mark Kotter, a stem cell biologist and founder & CEO of Bit Bio, discusses a unique opportunity to systematically interrogate the OS of human cell programming. Physicist and LIMS Fellow Ton Coolen describes mathematical models of gene regulation and epigenetic programming. Physicist and LIMS postdoc Alexander Mozeika talks about the statistical physics of the adaptive immune response and high-dimensional statistical inference. LIMS director and physicist Thomas Fink describes theoretical approaches to understanding the dynamics of network motifs and larger regulatory networks. This is followed by discussion on whether we have reached a tipping point where the mathematical sciences can help unleash fundamental insights into the operating system of life.


Scientists discuss the potential of mathematical modelling in biology across problems in cell programming, immunology and gene regulation.


Modelling in biology

Collective human behaviour describes emergent behaviour when individuals are influenced by the group to which they belong. The focus is often on behaviour that violates laws and social norms. This can range from the innocuous, such as fashion fads, to more serious instances, such as an anomalous voting or disproportionate responses to stress. For instance, it is now widely believed that Cambridge Analytica influenced both the US and UK democratic processes. In an era of social media storms and political demagoguery, understanding the workings of group dynamics, which can be hard to predict, has become increasingly urgent.

In this event, physicist Gioia Boschi from Kings College London explores opinion dynamics with emergent collective memory; physicist Carmen Cabrera Arnau from University College London discusses the dynamics of road accidents in urban areas; and mathematician Zahra Jafari from University College London talks about migration flows. After the talks, there is a general discussion on the scope for turning collective human behaviour into a quantitative science. Everyone is welcome.


Mathematicians and social scientists discuss quantitative models of group dynamics and emergent behaviour on 30 Jan from 6:30. All welcome.

Modelling collective human behaviour

How we go about solving a problem depends on how far into the future it is. When the problem is around the corner, we tend to react to it. But when it’s a long time away, we seek to transform it, putting to use new opportunities that arise in the interim. In other words, on short timescales we act as if our landscape is fixed, but on long timescales we try to shape our landscape so as to allay the concern. Understanding how to balance these strategies can help us manage distant threats, such as man-made and environmental catastrophes. When multiple people act together to shape the future with the right dynamical rules in place, the path to innovative solutions can be fast-forwarded – even in the absence of explicit cooperation. We call this process collective innovation.

In this dinner hosted by the BCG Henderson Institute, we discuss strategies for acting on multiple timescales, how to respond to distant threats and collective imagination. Participants include Brian Arthur, Thomas Fink, Simon Levin, Dan Levinthal, Mihnea Moldoveanu, Michael Nielsen and Martin Reeves, as well as industry practitioners.

A dinner and discussion about collective imagination, strategies for acting on multiple timescales and how to respond to distant threats.

Science of Business IV

Advanced machine learning algorithms provide a powerful set of tools for solving important real-world problems. As machine learning technology improves, these algorithms are becoming responsible for ever more critical decisions. But when they fail in unexpected ways, the consequences can be devastating and potentially lead to cascading failure. 

In this talk, Marc Warner, the CEO and cofounder of AI research company Faculty, talks about how we should manage AI safety both individually and on a collective scale. Clearing a path through the vacuous bullshit that the future of AI tends to accumulate, his conclusions are grounded in Faculty’s scientific research to make AI safe now and in the future. The talk is followed by a general discussion on how to ensure that AI and automated decision-making will be a net positive for businesses and society.


Marc Warner talks about how we should manage the safety of embedded artificial intelligence both individually and on a collective scale. 

Making sure Skynet behaves itself

The collective action problem describes a public good for which the benefits cannot be excluded to those who don’t contribute to it. When the benefits of the good are only realised by the next generation, as is the case with fighting climate change, the problem is compounded by the difficulties of long-term forecasting. But the situation is even more complex, because human innovation, which takes place in an expanding space of technological building blocks, is inherently hard to describe, much less predict.

In this dinner at the London Institute, we discuss innovation, technological change and new ways to combat climate change. Physicist and London Institute director Thomas Fink discusses speeding up innovation as an alternative to our current focus on environmental preservation. Technology expert and complex systems founder Doyne Farmer talks about how empirical regularities over past technological change can foretell the rate of change in the future. Building on these ideas, National Medal of Science winner Simon Levin discusses the collective action problem in climate change and how to overcome it.

A dinner and discussion about speeding up innovation, forecasting technological change and the collective action problem in climate change.

Science of Business III

Tatratea: a Slovakian tea-based liqueur. Ghorme sabzi: an Iranian kidney bean stew. Spaghetti alla puttanesca: Italian pasta with anchovies, olives and capers. These are some of the delicacies, each particular to their country of origin, contributed by everyone who attended the London Institute’s Christmas Party. Thomas Fink kept things real by grilling Texan cheeseburgers in the fireplace, followed by Antonia Tingey toasting marshmallows over a wood fire. 

After the feasting, a Meccano cracker construction competition ensued, which was won by Ton Coolen. Festivities continued into the small hours with drinks and conversation in equal measure.

The Institute’s Christmas Party continued into the small hours as members served their local delicacies and held a Meccano competition.

Christmas party goes crackers

Companies are composed of many individual employees that are collectively more than the sum of their parts. This super-additive aspect of companies can be thought of as a kind of organizational intelligence. Business leaders strive to build firms which are not only intelligent but can learn—and forget—new things as their goals and environments change. How do companies learn collectively and transform learning into action? How do they learn and act on multiple timescales simultaneously?

In this dinner hosted by the BCG Henderson Institute, we discuss different aspects of intelligent organizations. Martin Reeves, Global Director at Boston Consulting Group and Director of the BCG Henderson Institute, discusses commitment and flexibility in strategy for companies and natural systems. Simon Levin, Professor in Ecology and Evolutionary Biology at Princeton, talks about how "multi-clock" speed organizations act on multiple timescales. Mihnea Moldoveanu, Vice Dean of the University of Toronto School of Management, discusses learning and forgetting in the age of artificial intelligence.

A dinner and discussion about commitment and flexibility, acting on multiple timescales and learning and forgetting in the age of AI.

Science of Business II

Fires at the London Institute are a regular tradition. They form a focal point for conversation and a backdrop for blackboard calculations. Visitors are delighted and surprised to find a smouldering fire in London, but fires are perfectly permissible. Our fires are made from a range of fuels: hard and soft wood and coal and smokeless coal. (This is in contrast to the American tradition, where resinous soft woods are proscribed because fireplaces are rarely swept). The energy output of these fuels is largely proportional to their densities, but they differ in how much flame they emit and how long they last. In general, soft wood is to hard wood is to coal is to smokeless coal, where the amount of flame decreases along the progression but longevity increases.

The fireplace itself is in the seminar room and dates from the 18th-century. At the top of the marble surround is a classical lamp, in the manner of Robert Adam, which forms the Institute’s seal. In addition to fires for warmth and companionship throughout the year, the fireplace is occasionally used for barbeques—an even rarer central London sight.

Thomas Fink barbeques a Texan lunch in the popular seminar room fireplace as the London Institute celebrates American Independence Day.

Independence  Day BBQ

An ecosystem is a community of species in a single habitat. Interdependencies within the ecosystem mean the fate of one species can have surprising effects on the ecosystem as a whole. In a similar way, interconnected firms make up an economic ecosystem, and many of the challenges facing it are analogous to those confronting the natural ecosystem. Examples include resilience in the face of unexpected events, the agility to handle sudden environmental change, and the risk of cascading failure leading to ecosystem collapse.

In this dinner at the London Institute, we discuss the application of biological principles to problems in business and the environment. National Academy of Sciences biologist Simon Levin talks about evolutionary strategies for tackling intractable challenges in climate change. Former Government Chief Scientific Adviser Sir John Beddington discusses lessons from ecology on mitigating risk in complex ecosystems. Shifting to current events, New York Times columnist and Pulitzer Prize winner Thomas Friedman discusses reinventing the political process using evolutionary principles.

A dinner and discussion about applying principles from evolution and ecology to seemingly intractable problems in business and politics.

Science of Business I

A blockchain is a way to store a list of records that grows in time in a way that is difficult to falsify. The main idea is that each new record, along with its parent record’s codeword, is translated into a new codeword. Because it is infeasible to decipher a codeword, a record can’t be changed without changing all of the records that have descended from it. In cryptocurrencies based on blockchain, transactions are validated through a process called mining, which is incentivized with rewards to reduce transaction costs. Cryptocurrencies are the best-known applications of blockchain, but are there other uses for commerce and private data that could be just as transformative?

In this event, cryptographer and hedge fund manager Robert Sams talks about cryptocurrency stabilization; Simone Bronzini, co-founder of the blockchain company Chainside, discusses a threat model of blockchain applications; and physicist Andrea Baronchelli from London City University talks about modelling the cryptocurrency market. After the talks there is a general discussion on using blockchain technology for the public good.

Scientists and businessmen discuss the use of blockchain technologies across cryptocurrencies, commerce and the analysis of private data.

The future of blockchain

In one of the most damaging cyberattacks ever, the 2017 Wannacry ransomware spread across 150 countries. By encrypting sensitive data and demanding payment in Bitcoin, it held thousands of businesses hostage. Until it was brought down by a hidden kill switch, the identity of the hostage takers was protected by the blockchain technology behind the Bitcoin cryptocurrency. More crippling ransomware attacks are sure to follow. But how does ransomware work, and how can we protect against it? What is the blockchain technology behind the cryptocurrencies funding it, and how can it transform business? 

In this symposia organized by Elli Streit and Ben Lynch from the LIMS Ventures board, leaders in intelligence, defence, business and academia help answer these questions. Ben Addis from the Serious Organised Crime Agency opens with an introduction to ransomware. Charly Shugg and Jeff Birnbach from Sylint give a strategic vision for cybersecurity. Simone Bronzini, co-founder of Chainside, introduces blockchain and cryptocurrency. Last, Nicolas Courtois from UCL talks about stealth and anonymity in blockchains.

Leaders in intelligence, defence, business and academia discuss the technology behind ransomware and the cryptocurrencies that fund it.

Ransomware  and blockchain

Artificial neural networks were inspired by simple models of computation in the brain. Despite rapid progress in understanding them theoretically, artificial neural networks did not live up to their early promise in terms of practical results. Only recently have they begun to show potential for performing seemingly intelligent tasks. On the other hand, biological neural networks are capable of extraordinary computational feats, but how they achieve it remains a mystery. Do artificial networks really offer insight into brain function, or are they a distinct framework for computation in their own right?

In this event, Thomas Parr from University College London talks about active inference and computational neuropsychology. Grace Lindsay, also from UCL, discusses using convolutional neural networks to study biological visual attention. Alexander Mozeika from King’s College London talks about the statistical physics of feedforward Boolean networks. After the talks there is a general discussion on whether and how artificial neural networks can help us understand the workings of their biological counterparts.

Physicists and neuroscientists and discuss how artificial neural networks can shed light on the working of their biological counterparts.

Neuroscience and  artificial intelligence

One of the most puzzling things about physics is that the mathematics that describes the universe is surprisingly beautiful. This language of the universe advances in a way that is both deeper and more elegant then would seem humanly reasonable, despite being borne of human consciousness. As Roger Penrose explains it, “We have a closed circle of consistency here: the laws of physics produce complex systems, and these complex systems lead to consciousness, which then produces mathematics, which can then encode in a succinct and inspiring way the very underlying laws of physics that gave rise to it.” Because the subjects are so intertwined, a guiding principle of the London Institute is to keep them both under one roof.

In this talk Charles Epstein talks about the fruitful but factious relationship between physics and mathematics from the 17th century until now. He discusses the difficulties met when physicists and mathematicians collaborate, the role of intuition in each subject, and how they interpret the concept of “proof”. He speculates on how the two fields will influence each other into the future.

Charles Epstein talks about the longstanding fractious but fruitful relationship between pure mathematics and mathematical physics.

Pure mathematics meets  mathematical physics

How do you describe the behaviour of hair? Leonardo da Vinci thought it flowed like water, but modeling realistic hair in computer animated films is challenging. Hair fibers are elastic filaments with random intrinsic curvature, like cotton and fiberglass. A bundle of fibers is subject to the combined effects of bending elasticity, gravity and orientational disorder. Despite the ubiquity of fiber bundles in the natural and man-made world, a mathematical description of how a bundle behaves has remained elusive.

In this talk Robin Ball develops a mathematical model of the behaviour of a bundle of fibers and applies this formalism to the iconic problem of the ponytail. The elasticity, gravity, and disorder are recast as a differential equation for the envelope of the ponytail bundle, in which the compressibility enters through an equation of state. From this, it is possible to identify the balance of forces in various regions of the ponytail, extract a remarkably simple equation of state from laboratory measurements of real ponytails, and relate the pressure to the random curvatures of individual fibers.

Robin Ball talks about a theoretical model of fibers in which their elasticity and curliness produce the characteristic shape of a ponytail.

Ponytail physics

Technology changes through an evolutionary process in the sense that it satisfies Darwin and Wallace’s key properties: descent with modification and selection. However, the process through which change takes place in technology is very different from that in biology. For example, biology mutates in all directions, but in technology variation is more directed. There are also differences is the available data and our knowledge of it. In biology we have an accurate phylogeny, and the fossil record indicates how this changed through time. For technology we have historical observations of when inventions appeared, but know much less about the forces that influenced them. There are several taxonomies provided by patent processes but they are far from concordant.

There are nonetheless some statistical laws about technological performance, such as Wright’s law and a variety of Moore’s laws for different technology sectors. In this talk Doyne Farmer summarizes the state of the art of our understanding of technological evolution and sketches some of the problems that need to be solved to create a better theory. 

Doyne Farmer talks about what technology is and how it evolves and our improving ability to forecast technological change into the future.

Evolution of  technology

A multifractal is a generalization of a fractal in which there is not a single scaling exponent but a continuous spectrum of exponents which depends on the length scale. Multifractals were originally conceived to describe turbulence in fluids, but have since developed into one of the main tools of econophysics. A collection of related studies, econophysics employs statistical physics to investigate the distribution of financial returns, macroscopic models of financial markets, agent-based models of the economy and the network structure of financial institutions.

In this talk Tiziana Di Matteo describes the use of multifractals to study financial data. Two main elements define the complexity of financial time series: multifractality, which is associated with the behavior of each variable and how it scales in time; and the structure of dependencies between time series, associated with the collective behavior of the whole set of variables. So far, these two manifestations of complexity have been investigated separately. Here, by considering both simultaneously, a theory emerges describing how they relate.

Tiziana Di Matteo talks about the interdependence of multifractal financial time series and a new way to understand and forecast them.

Multifractal finance

The Grand Tour of Science is a comprehensive account of modern science in seven two-hour lectures for the public. The lectures are in two parts, with drinks and discussion before, in between and after.

This lecture covers:
• Shannon’s information theory
• Bayesian versus maximum likelihood statistics 
• The problems of ‘big data’
• True patterns versus overfitting
• Modern information-driven medicine 

Mark Girolami talks about how information, inference and data analysis drives the digital revolution in part 7 of our Grand Tour of Science.

The science of information

The Grand Tour of Science is a comprehensive account of modern science in seven two-hour lectures for the public. The lectures are in two parts, with drinks and discussion before, in between and after.

This lecture covers:
• The standard model: particles and interactions
• The Higgs and its mysteries
• Problems and puzzles
• Unification and supersymmetry
• Superstrings and M-theory

Neil Lambert talks about subatomic particles and the elusive search for a theory of everything in part 6 of our Grand Tour of Science.

High energy  physics

The Grand Tour of Science is a comprehensive account of modern science in seven two-hour lectures for the public. The lectures are in two parts, with drinks and discussion before, in between and after.

This lecture covers:
• What is life?
• The beginnings of molecular biology
• Crystals, symmetry and X-ray crystallography
• Discovery of the structure of DNA
• Towards synthetic biology

Brian Sutton talks about the path to understanding life, molecular biology and synthetic biology in part 5 of our Grand Tour of Science.

DNA and the human genome

The Grand Tour of Science is a comprehensive account of modern science in seven two-hour lectures for the public. The lectures are in two parts, with drinks and discussion before, in between and after.

This lecture covers:
• Conundrums of the atom and black-body radiation 
• Wave mechanics and matrix mechanics
• Heisenberg’s uncertainty principle
• Discovery of antimatter
• Quantum information and materials science 

Chris Pickard talks about how Nature’s mysterious non-determinism is captured by quantum mechanics in part 4 of our Grand Tour of Science.

Quantum  theory

One new thing often leads to another. Such correlated novelties are a familiar part of daily life. They are also thought to be fundamental to the evolution of biological systems, human society and technology. By opening new possibilities, one novelty can pave the way for others in a process that Kauffman has called “expanding the adjacent possible”. However, correlated novelties and how they change over time have yet to be quantified empirically or modeled mathematically. Nowadays, thanks to the availability of extensive longitudinal records of human activity online, it has become possible to test whether everyday novelties crop up by chance alone, or whether one truly does pave the way for another.

In this talk Vittorio Loreto proposes a simple mathematical framework that mimics the process of exploring a physical, biological or conceptual space that enlarges whenever a novelty occurs. He tests the predictions on four data sets of human activity. He also highlights future directions: the interplay between individual and collective effects and the different mechanisms supposedly leading to innovation.

Vittorio Loreto talks about the dynamics of correlated novelties in the evolution of biological systems, human society and technology.

Dynamics of  correlated novelties

The Grand Tour of Science is a comprehensive account of modern science in seven two-hour lectures for the public. The lectures are in two parts, with drinks and discussion before, in between and after.

This lecture covers:
• Non-integer dimensions and scale invariance 
• Riemannian geometry
• Groups and crystals
• Aperiodicity and Gödel incompleteness
• Turing machines and non-computability

Andrew Green talks about the theory of relativity, cosmology and the structure of the universe in part 3 of our Grand Tour of Science.

Relativity and  the universe

Thomas Fink talks about radical new mathematical developments that set the stage for modern physics in part 2 of our Grand Tour of Science.

Revolutions  in mathematics

The Grand Tour of Science is a comprehensive account of modern science in seven two-hour lectures for the public. The lectures are in two parts, with drinks and discussion before, in between and after.

This lecture covers:
• The hypothesis-prediction-experiment loop
• Tycho Brahe and the role of data
• The scientific revolution of the 17th century
• Physics from Gallileo to Maxwell
• The character of physical laws

Robert Farr talks about the emergence of science from astronomy and the rise of classical physics in part 1 of our Grand Tour of Science.

Classical quantitative science

BBC science presenter Steve Mould bought a 50m long chain as a prop and stored it in a jar. To his surprise, he found that if he dangled the end of the chain over the rim of the jar, the entire chain would spontaneously flow down to a pile on the floor. More surprisingly, it leapt up in a sustained arc above the jar. Mould made a video of his chain which went viral on YouTube. But despite millions of views and much speculation in illustrious physics departments around the world, no one could explain why the chain rises above the jar.

In this talk, John Biggins explains how he and Mark Warner solved the mystery of the leaping chain. To do so, he first revisits and repairs textbook notions about how chains are picked up from surfaces. He shows that a chain fountain spontaneously forms in the shape of an upside-down catenary, that is, the inversion of the shape of a hanging chain. This is the optimal shape for an arch of perfect compression and has been used by architects and engineers from Hooke and Wren to Gaudi. But the chain fountain is a new structure: an arch of perfect tension stabilized by motion.

John Biggins talks about how he solved the mystery of the chain fountain, in which a chain spontaneously leaps up as it flows out of a jar.

Unraveling the  chain fountain

Is physics creative? Many people think of it as the opposite: all left brain and no right brain. But when it comes to scientific discoveries, mathematical prowess is only one side of the coin. Fundamental advances rely on finding links, usually mathematical in form, between seemingly disconnected fields—an intrinsically creative act.

In this talk, Thomas Fink gives a personal account of how physicists discovery theories by building systems of the world. He presents three tales from his own experience: about discovering tie knots, tiling the plane and learning to dance. In the first, he explains how systems can be found almost everywhere, if we look closely enough: mathematical structure lurks behind the ordinary as well as the remarkable. In the second, he illustrates how in the world of systems, miracles can happen: our intuition is all but useless when it comes to how the universe works, and there are extraordinary surprises to be had. In the third, he describes the dangers of trying to systematize human aspects of life that resist mathematical insight: not everything has a system, and that’s OK.

Thomas Fink talks about physicists’ inner drive to systematize the world around them and the role of imagination in building theories.

Calculation and creativity

Chris Pickard talks about materials under conditions so extreme they cannot be studied in the laboratory in our Science and Society series.

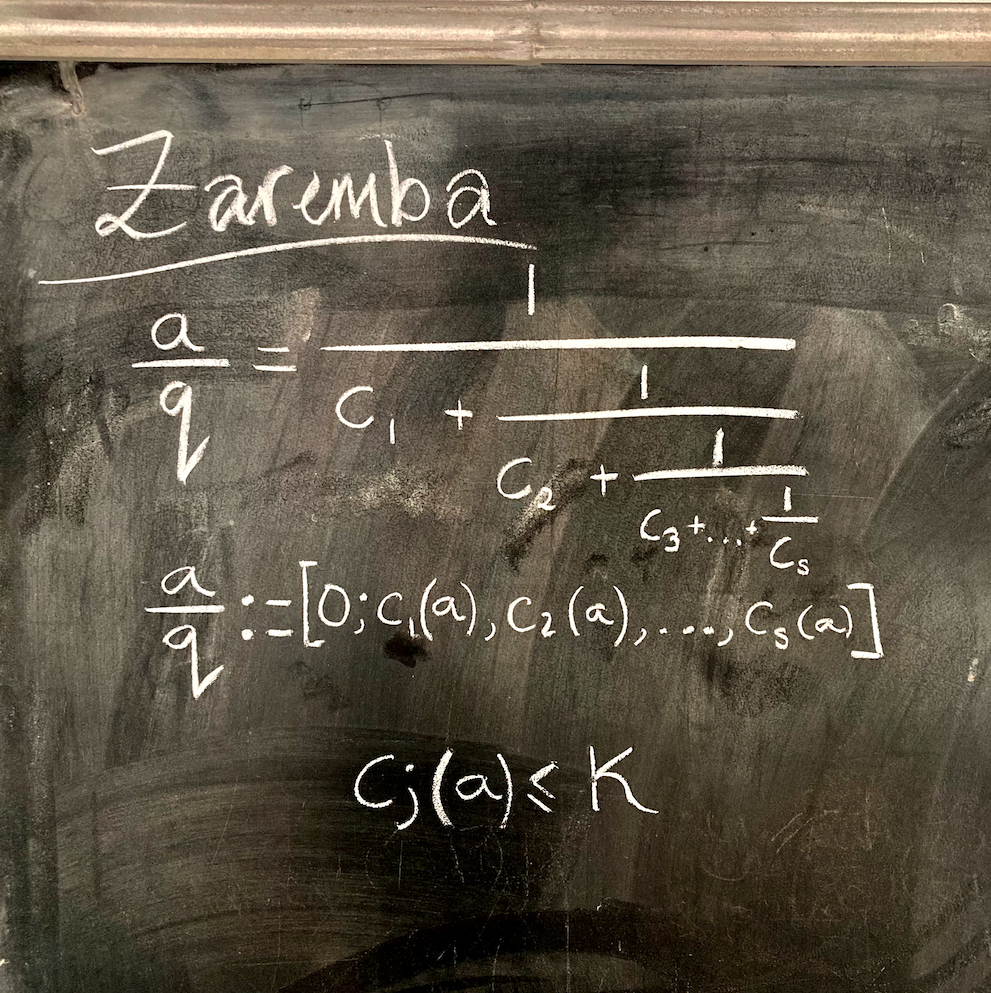
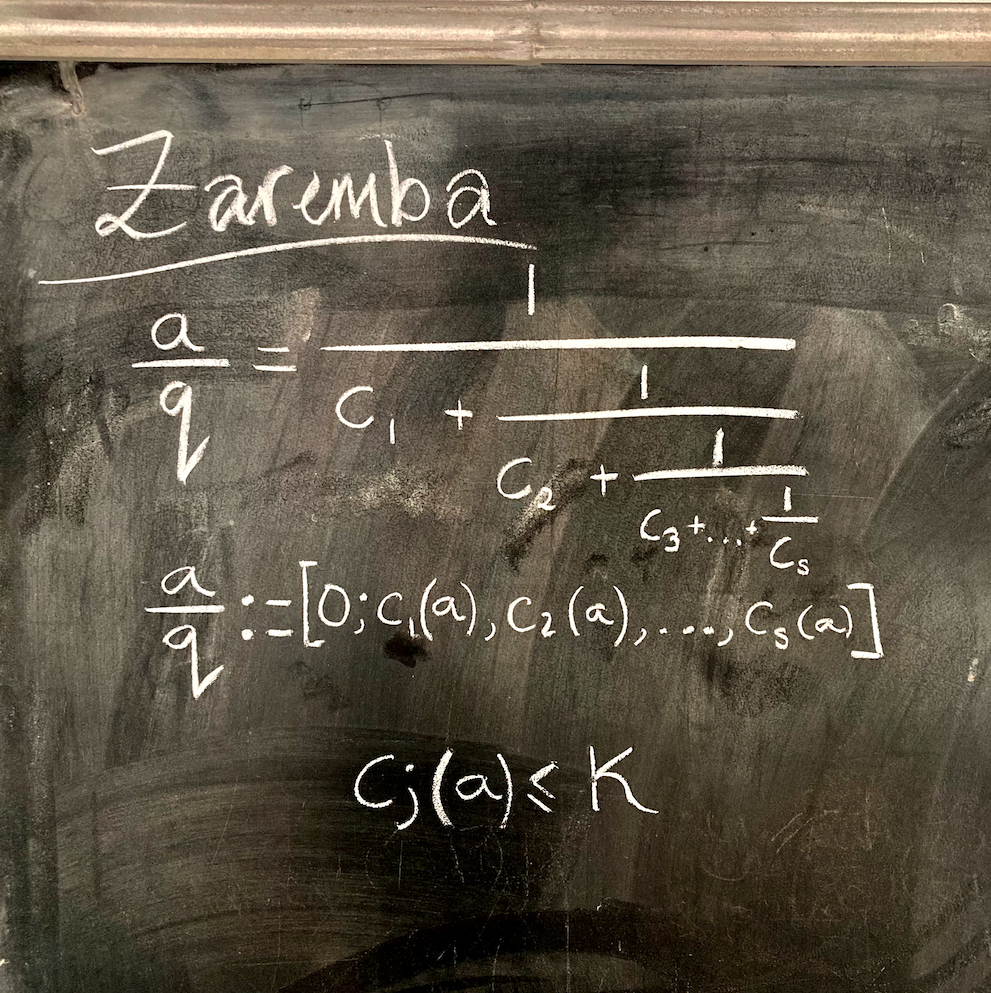
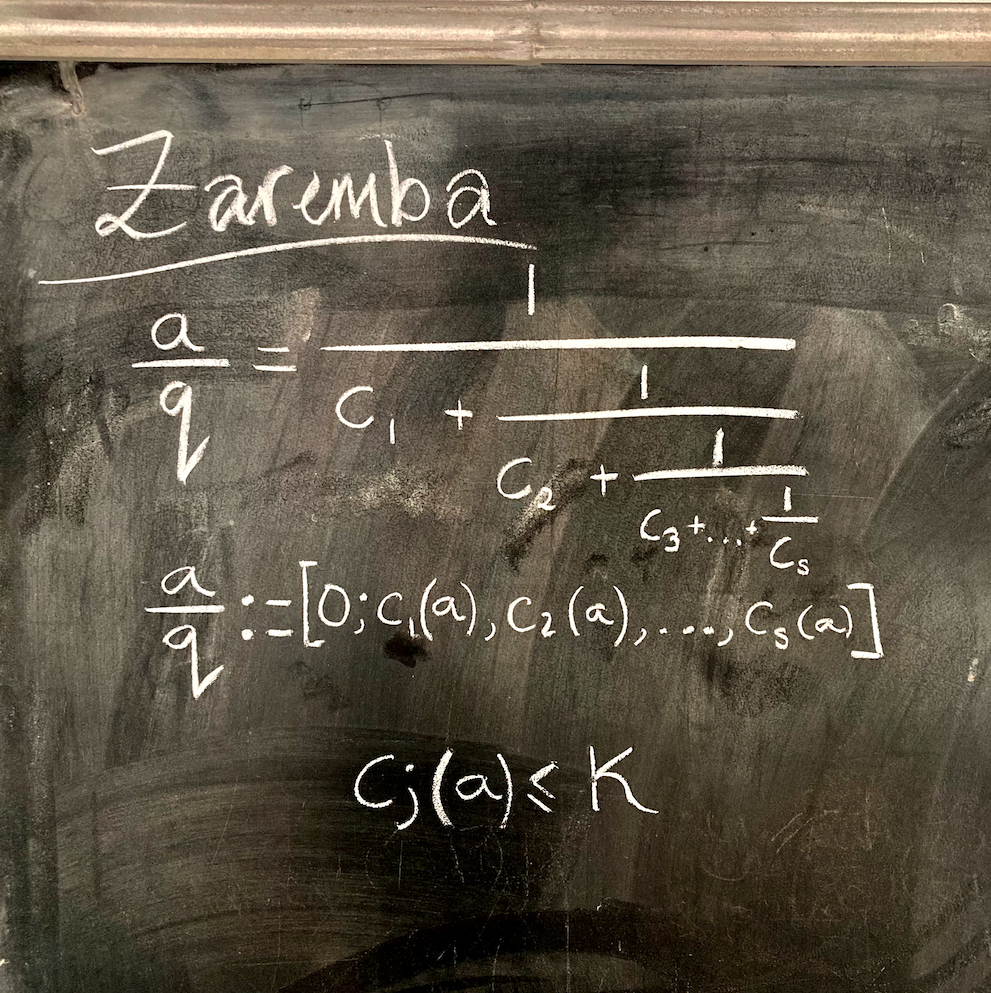
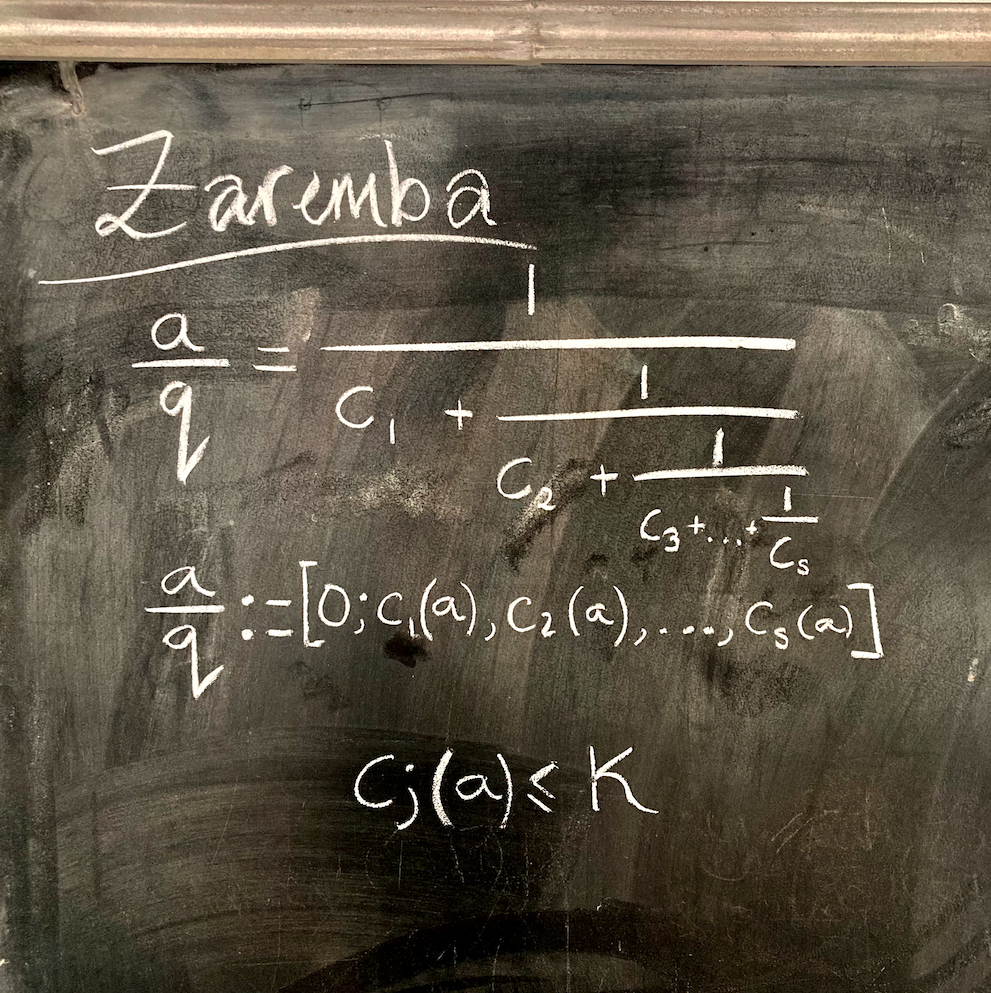
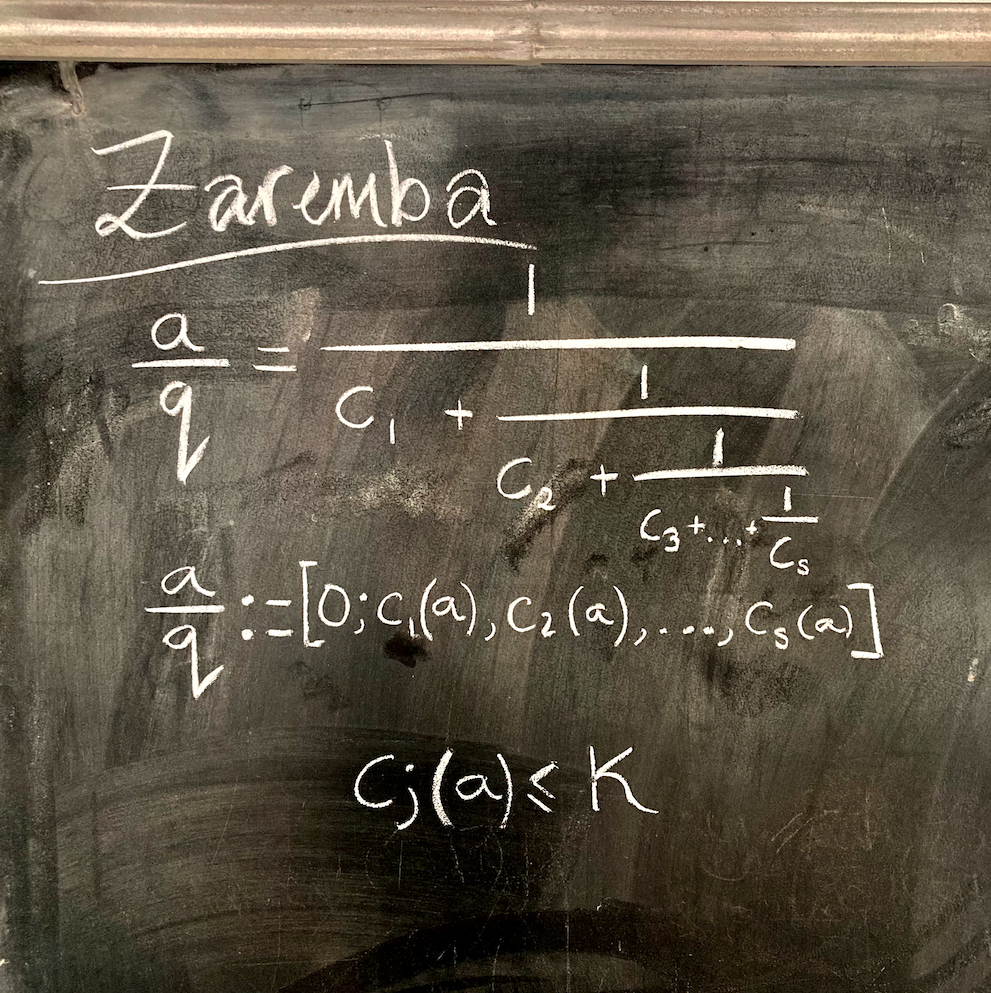
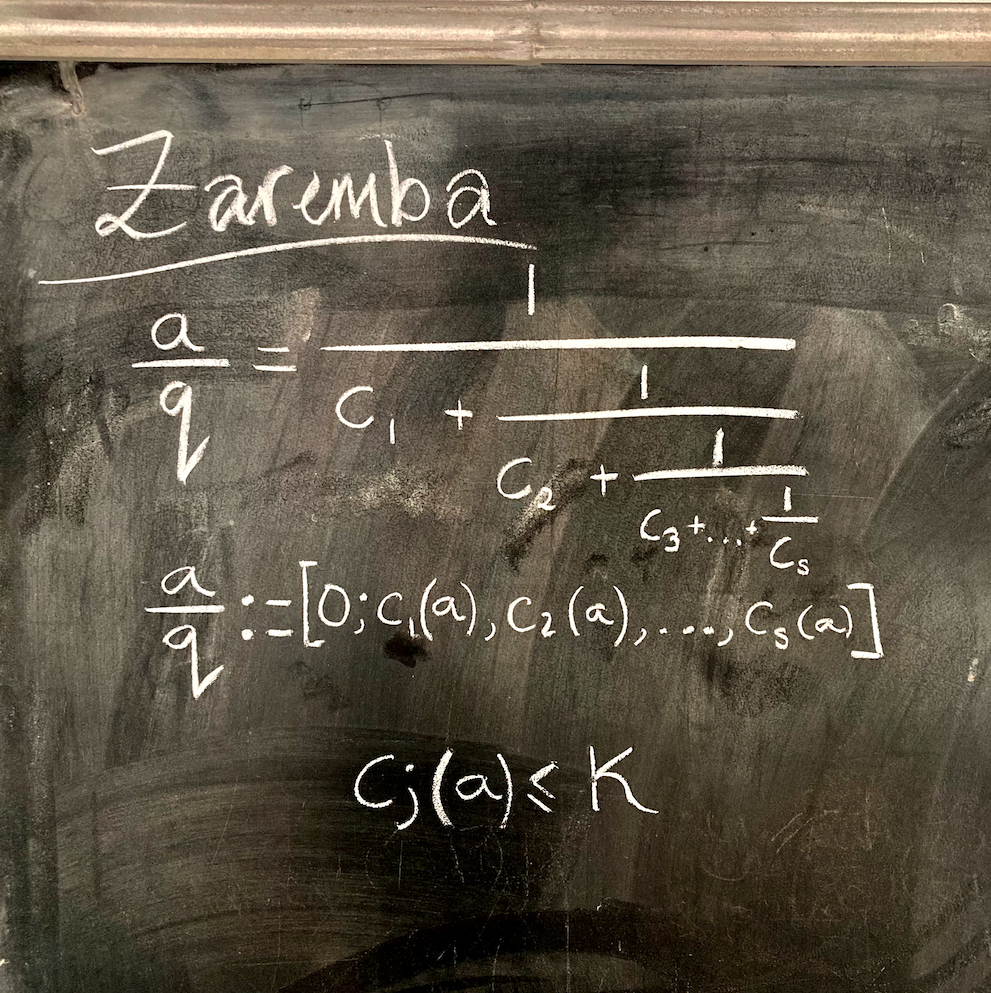
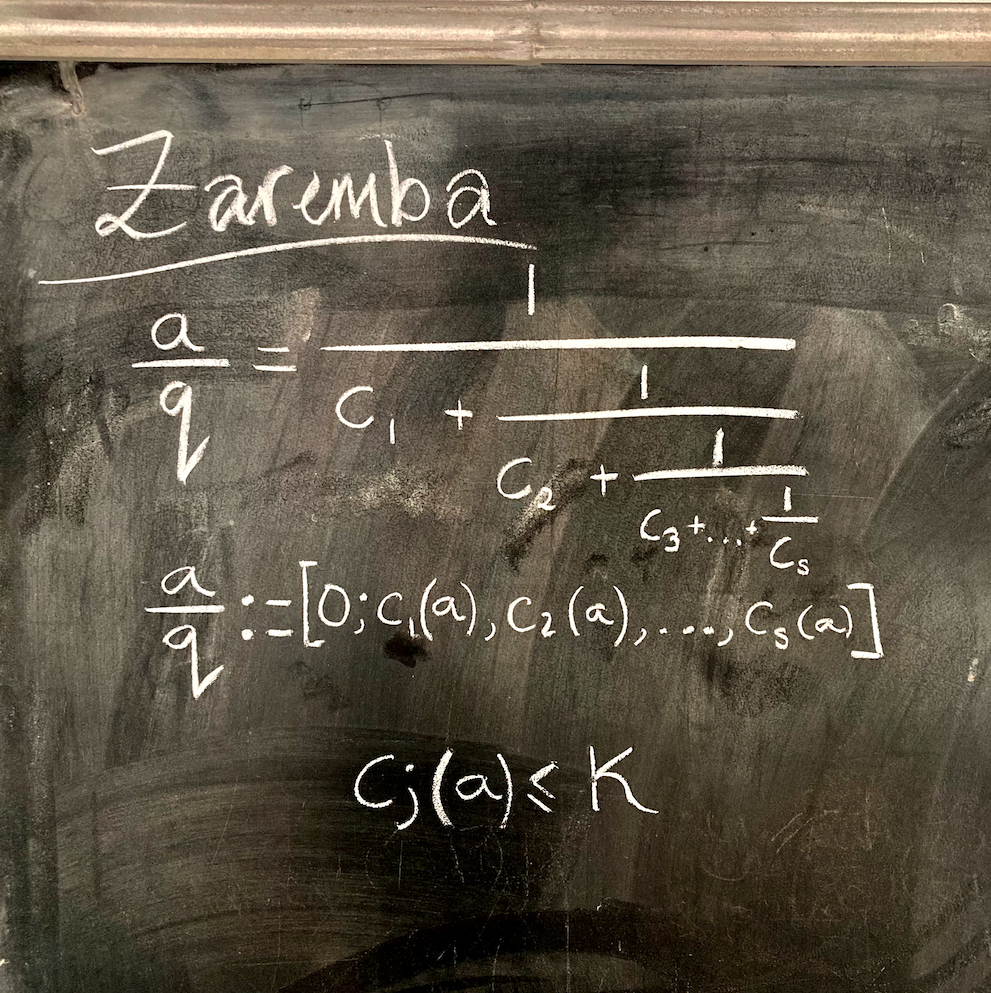
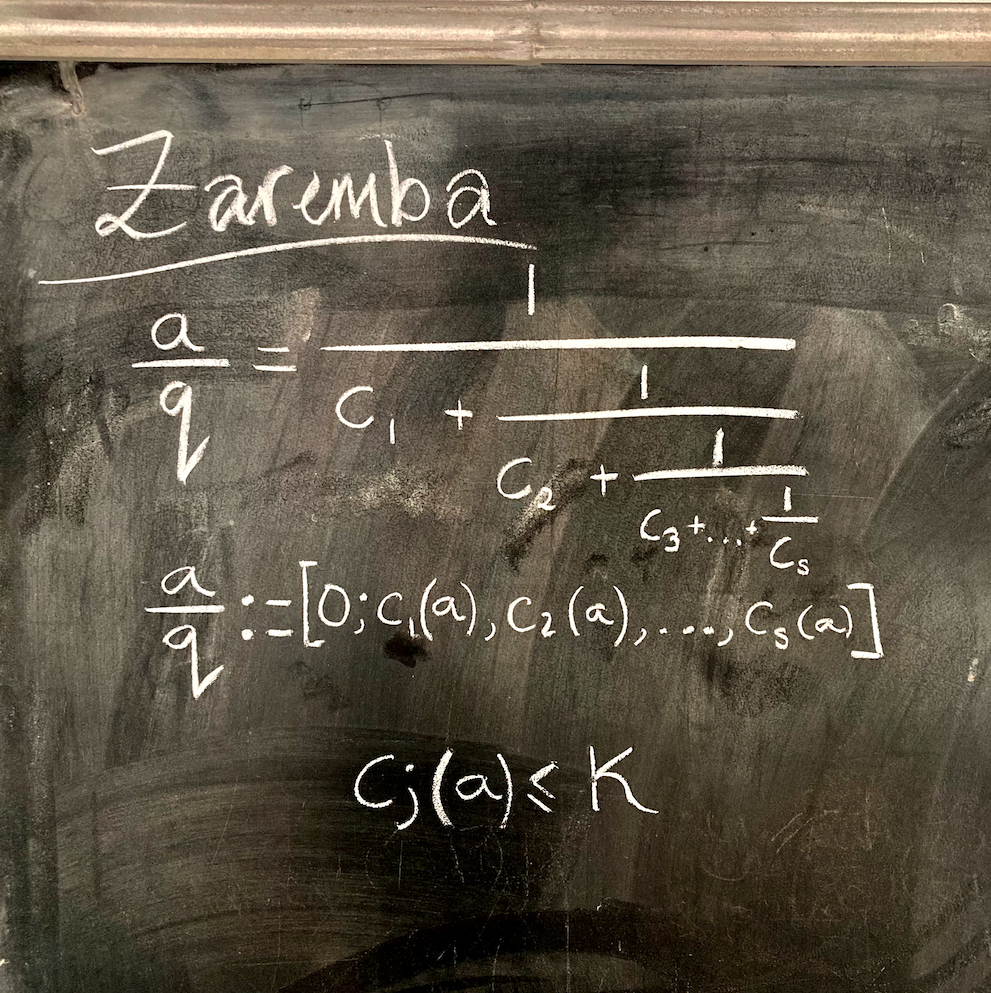
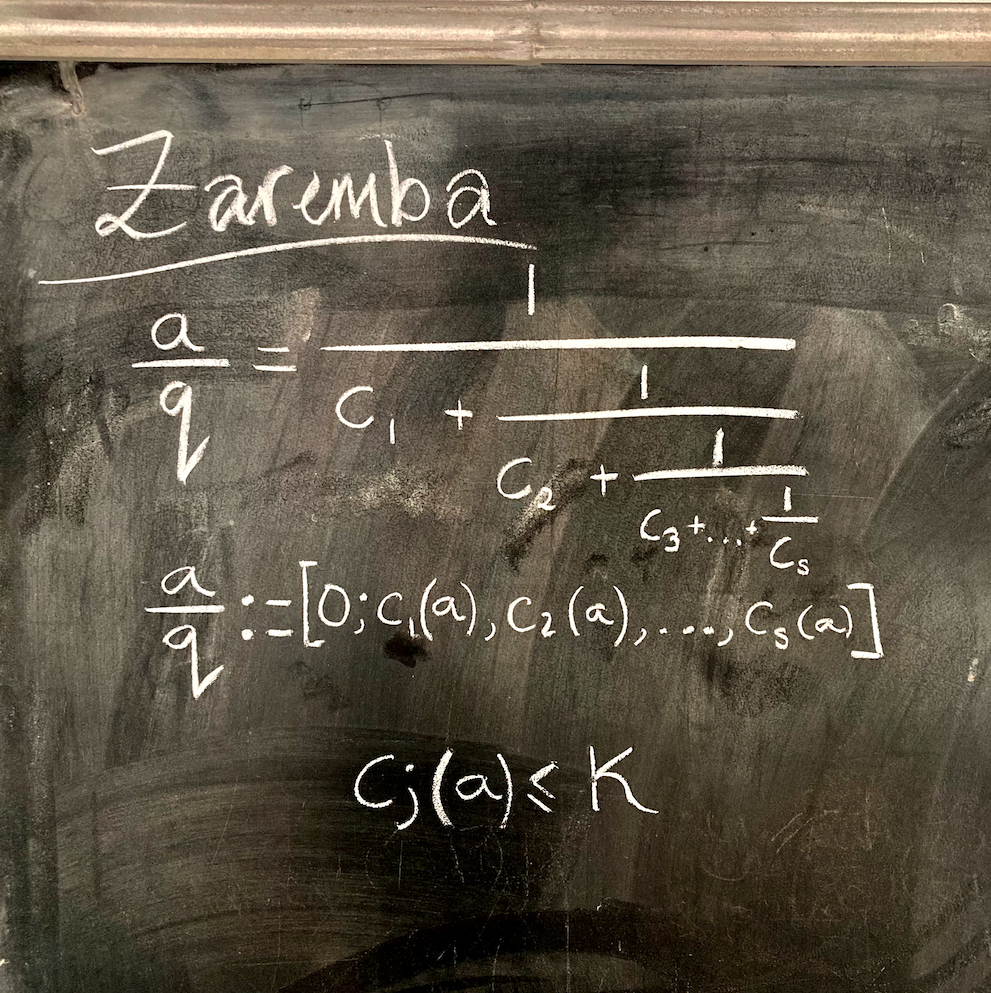
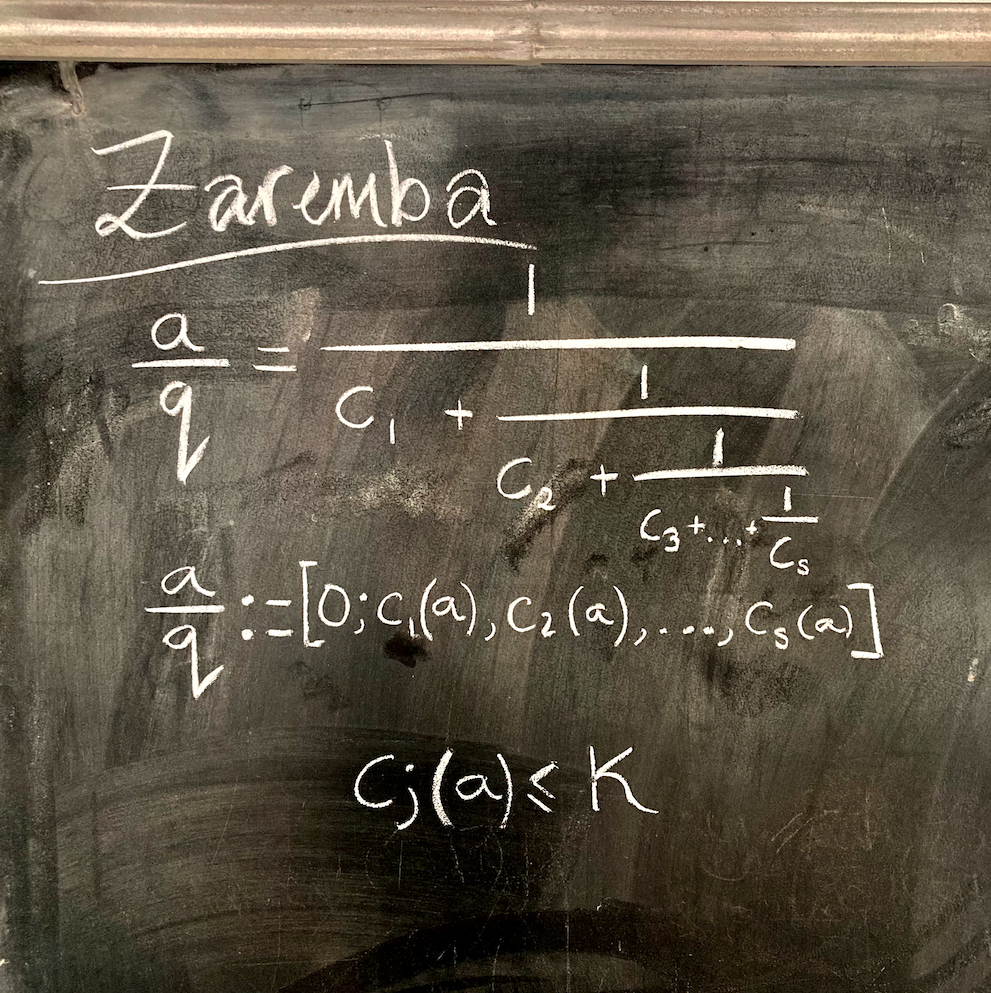
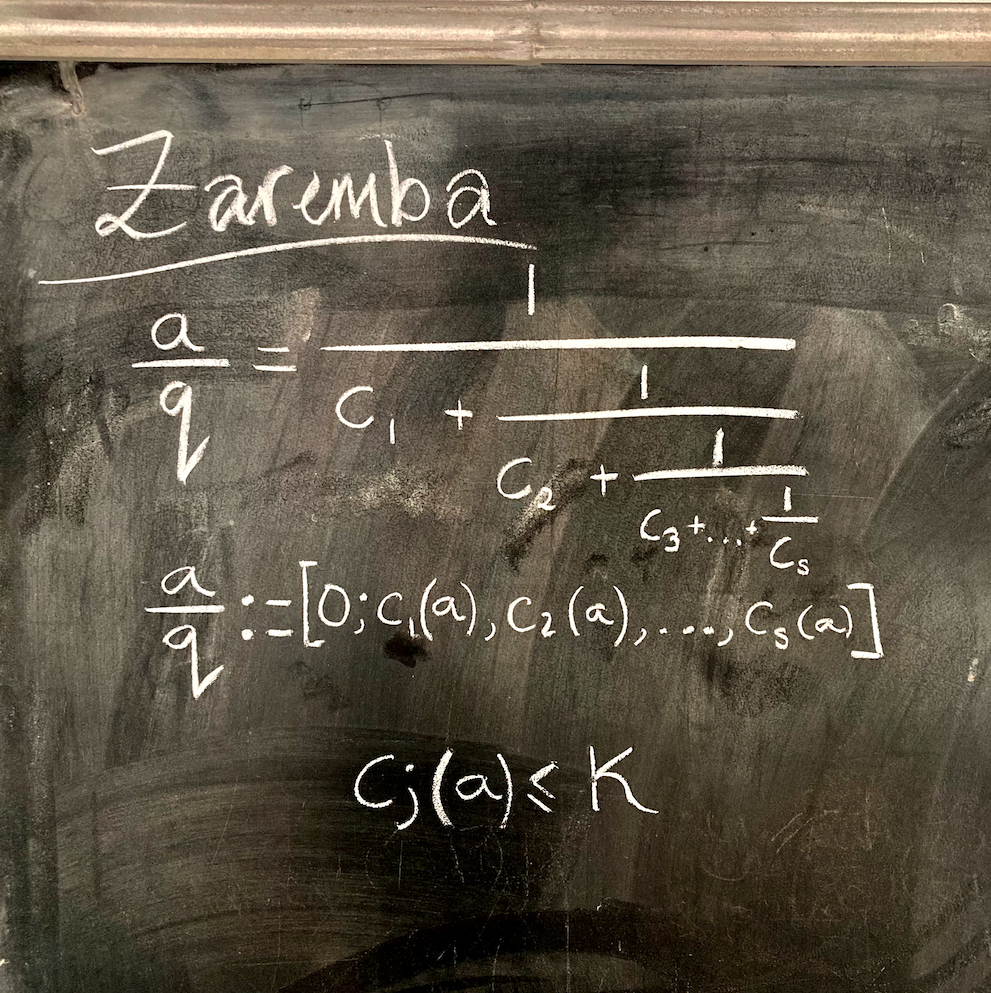
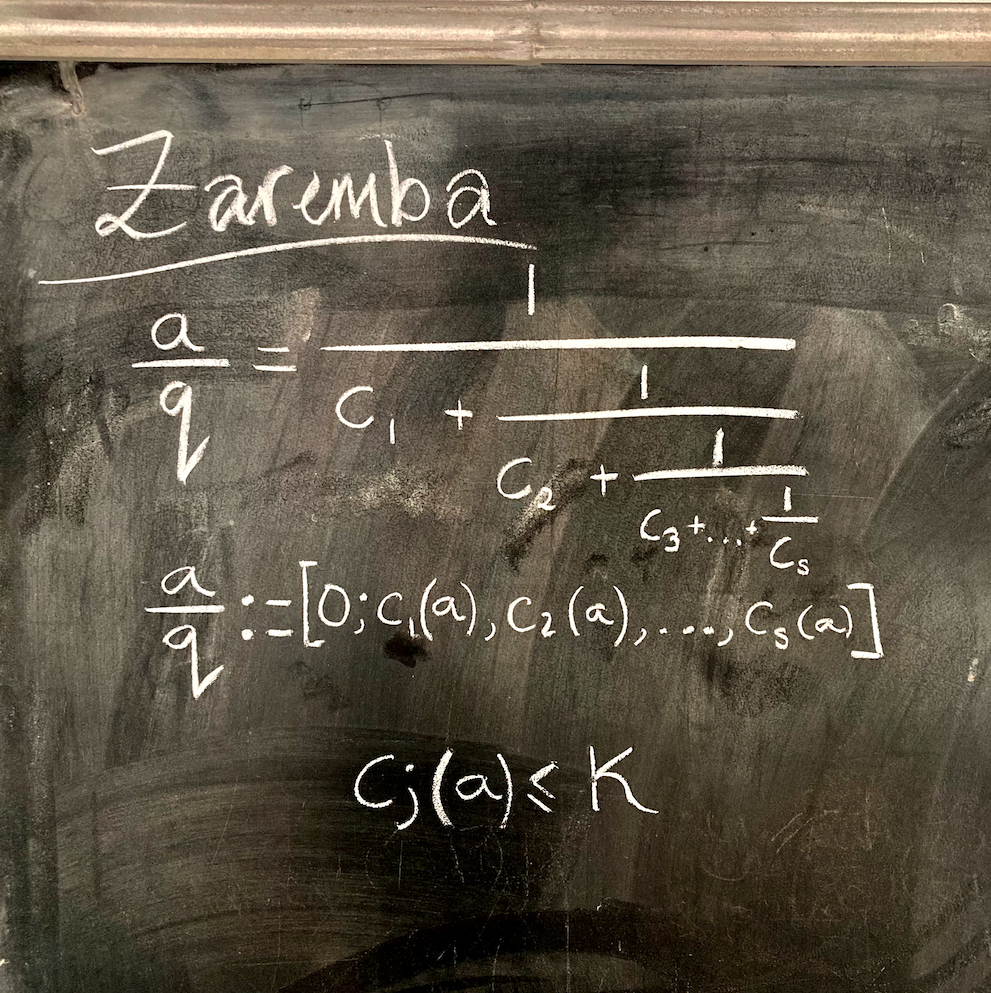
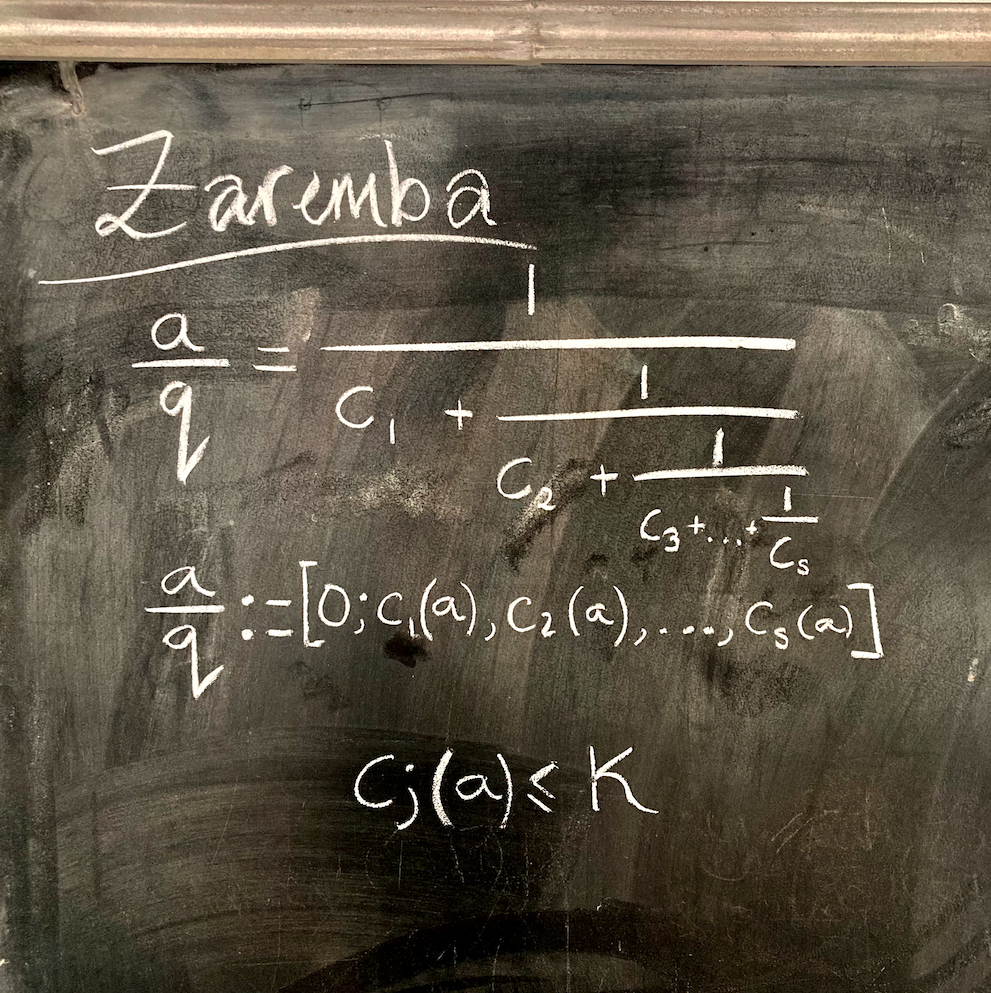
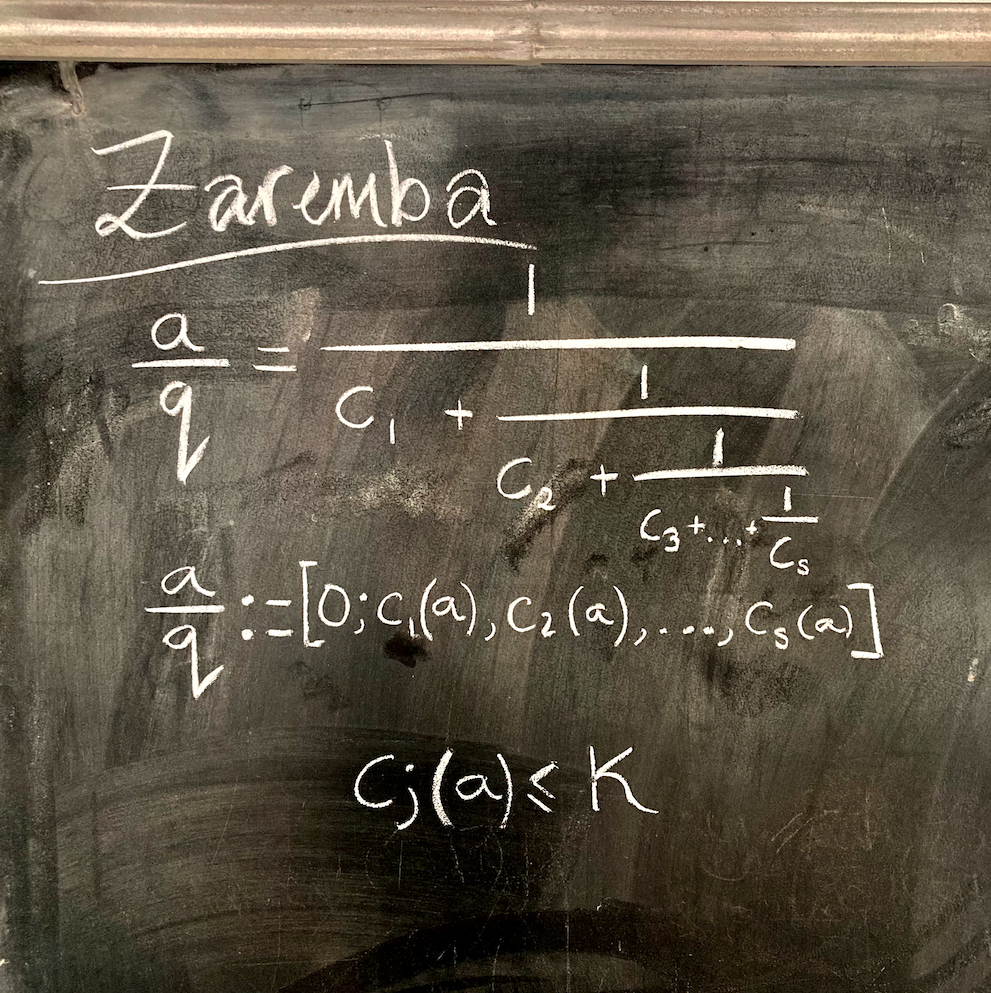
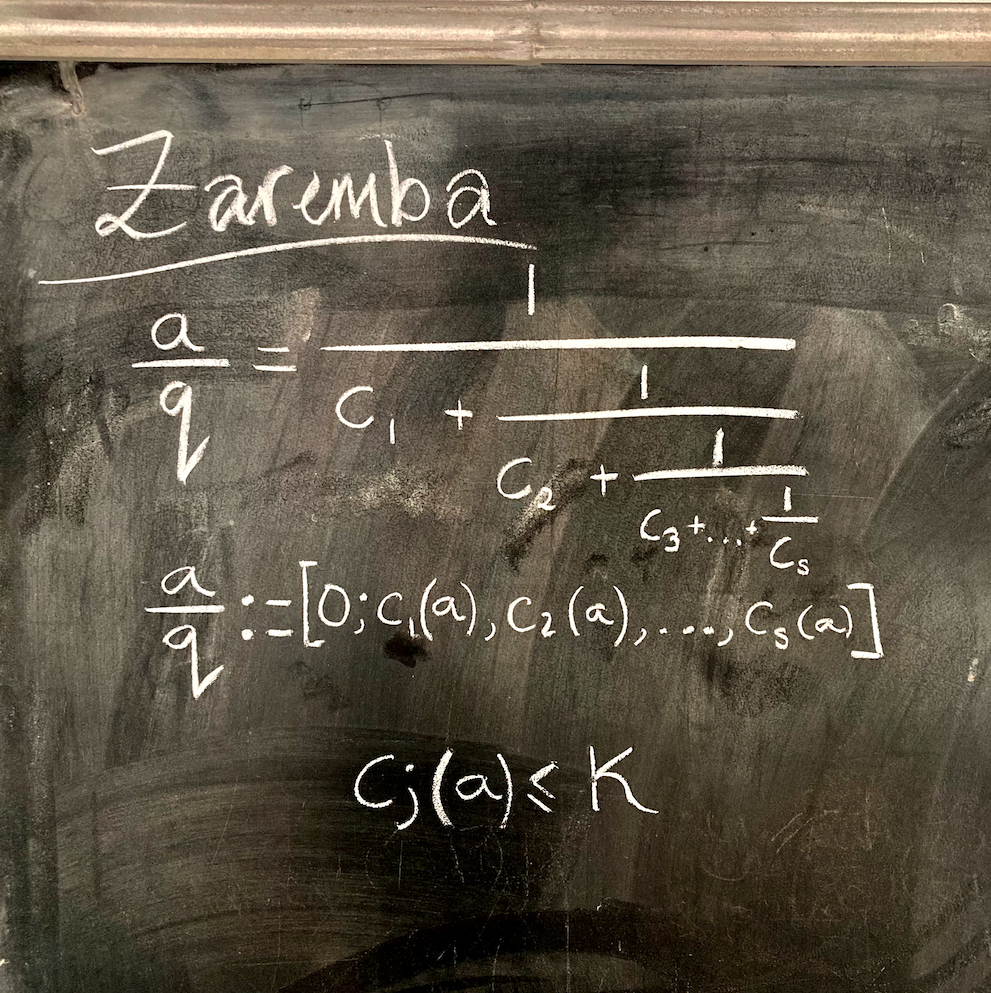
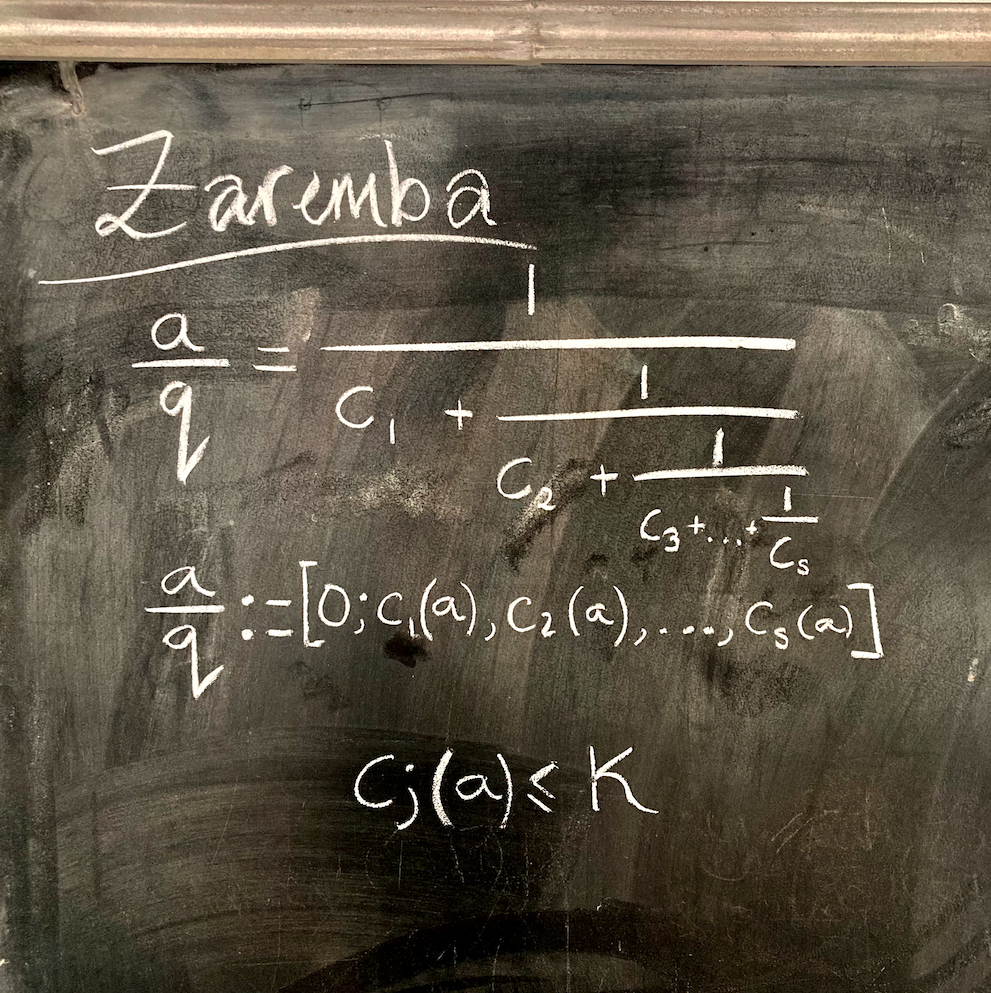
A new bound concerning Zaremba’s conjecture

5 pm, 29 Mar 2023

Event info

Speakers