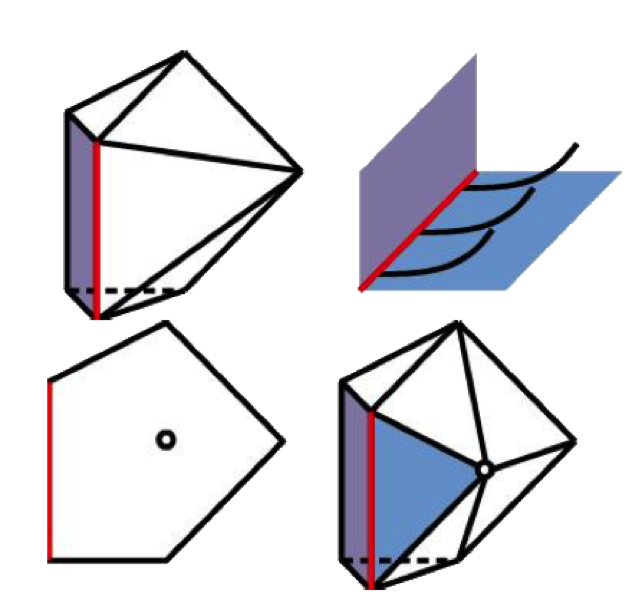
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"
Image for the paper "Slightly degenerate systems of polynomial equations"

Slight degeneration

Newton polytopes are used to study systems of general polynomial equations, which consist of given monomials with generic coefficients. We describe what happens to solutions of these systems when the coefficients slightly degenerate.

Schön complete intersections

Arxiv (2024)

A. Esterov, L. Lang

Arxiv (2024)

A. Esterov, L. Lang