Maximum percolation time in two-dimensional bootstrap percolation
A simple formula gives the maximum time for an n x n grid to become entirely infected having undergone a bootstrap percolation process.
SIAM Journal on Discrete Mathematics 29, 224 (2015)
F. Benevides, M. Przykucki
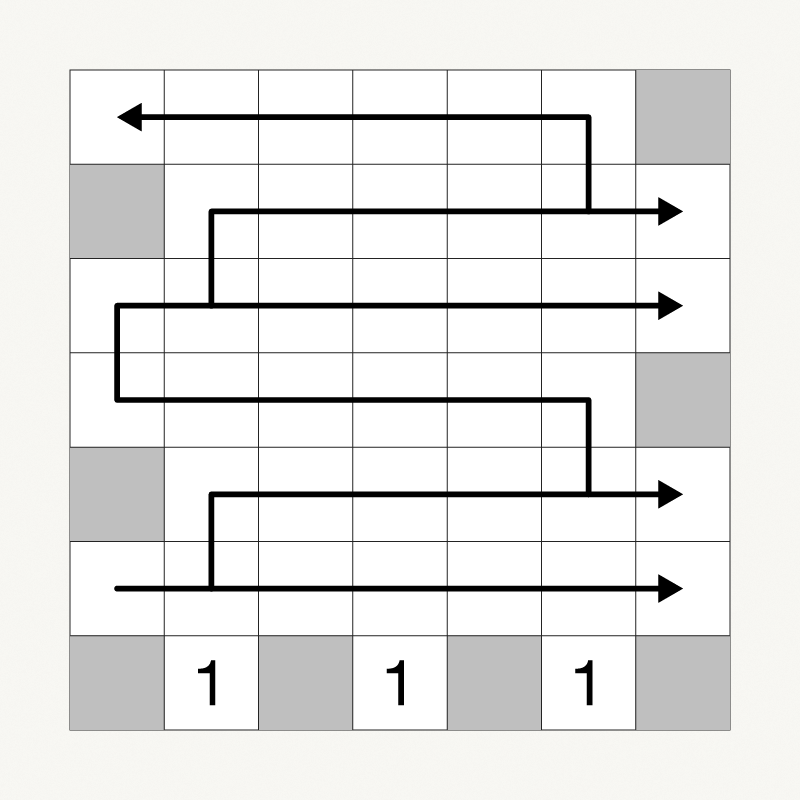















We consider a classic model known as bootstrap percolation on the n × n square grid. To each vertex of the grid we assign an initial state, infected or healthy, and then in consecutive rounds we infect every healthy vertex that has at least 2 already infected neighbours. We say that percolation occurs if the whole grid is eventually infected. In this paper, contributing to a recent series of extremal results in this field, we prove that the maximum time a bootstrap percolation process can take to eventually infect the entire vertex set of the grid is 13n^2/18 +O(n).