When Richard Feynman died in 1988, his last blackboard bore a curious note to himself: “To learn: Bethe Ansatz.” The Bethe Ansatz, introduced by Hans Bethe in 1931, is a method for finding the spectra of Hamiltonians in quantum integrable systems such as the Heisenberg magnet. For decades it helped produce astonishing results and conjectures, though no one quite knew why it worked.

In this talk, Prof. Edward Frenkel revisits this enduring mystery. In collaboration with Boris Feigin and Nicolai Reshetikhin, he reinterpreted the Bethe Ansatz through the lens of the geometric Langlands correspondence, expressing its spectra in terms of mathematical objects known as opers. This framework led to powerful generalisations involving q-characters of quantum affine algebras and q-opers, bridging quantum physics and modern geometry.

Prof. Frenkel explores these ideas and reflects on why the Bethe Ansatz—an old key to new symmetries—still stood at the top of Feynman’s list.

## Event information
The event takes place on Thursday 11 December at the London Institute for Mathematical Sciences, which is on the second floor of the Royal Institution.

Edward Frenkel illuminates Feynman’s final quest—to learn the Bethe Ansatz—with fresh insights from the geometric Langlands correspondence.

Feynman’s last wish

Speaker

Quantum integrable systems: from Bethe Ansatz to Langlands duality

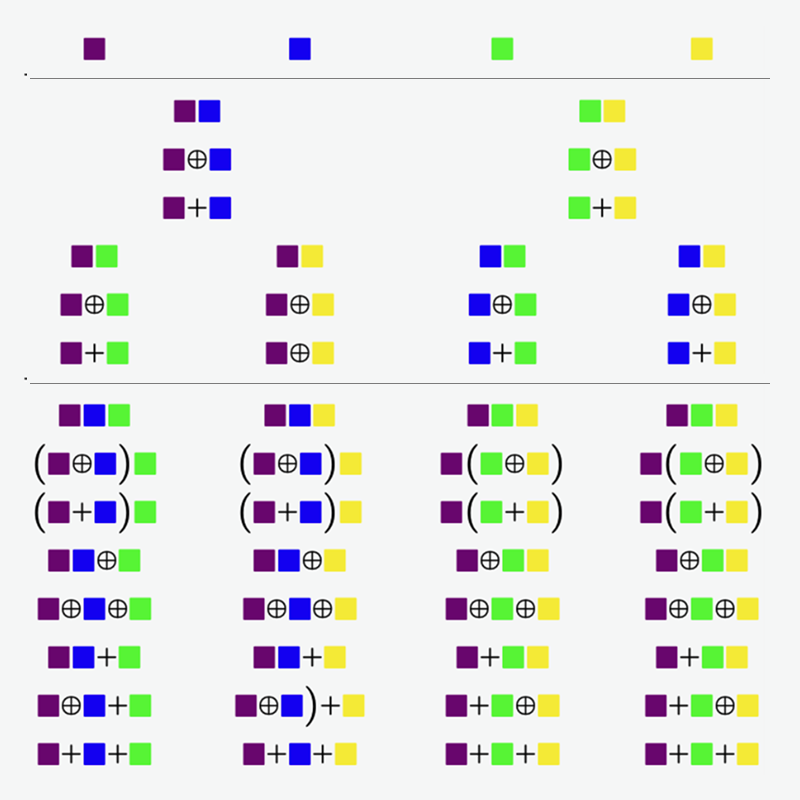
By analytically studying the repeated composition of simple Boolean functions, Dr Thomas Fink uncovers the spontaneous emergence of a law of parsimony. It is the first exact solution of a nontrivial input-output map, and suggests an explanation for why neural networks are biased towards simplicity in the models that they generate. The general result applies whenever composition of more than one input occurs.

[Dr Thomas Fink](https://lims.ac.uk/thomas-fink/) is the founding Director of the London Institute and Charge de Recherche in the French CNRS. He studied physics at Caltech, Cambridge and École Normale Supérieure. His work includes statistical physics, combinatorics and the mathematics of evolvable systems.

Our director Thomas Fink explains why the repeated application of simple logics induces a bias towards simplicity, with applications to AI.

Why AI works

Why AI works: The spontaneous emergence of a law of parsimony

To many, science appears as a kind of modern magic—the only magic that works. In the Soviet Union, an officially atheist state, science was elevated even further, becoming a substitute for religion.  The DAU project began as a biopic of Lev Landau, the Nobel Prize–winning physicist and icon of Soviet science. But it evolved into something far more ambitious: a vast social and artistic experiment exploring what it means to be Soviet, to be modern and to believe in science. 

As part of the project, hundreds of participants lived and worked inside a reconstructed Soviet research institute, their lives filmed in an unprecedented exploration of the scientific worldview. Among the works born of the ongoing project was *DAU. Natasha*, which won the Silver Bear at the Berlin International Film Festival in 2020.

In this talk, Prof. Dmitry Kaledin offers a rare insider’s view of DAU—from its portrayal of Soviet scientific culture to its deeper inquiry into the meaning of science itself.

## Event information
The event takes place on Thursday 27 November at the London Institute for Mathematical Sciences, which is on the second floor of the Royal Institution. To book a place, register [here](https://tally.so/r/3lokj6).


Dmitry Kaledin reflects on the DAU project—an audacious theatrical experiment probing science and belief in the Soviet Union and beyond.

The magic of DAU

DAU: the magic that works

Matter and fundamental forces are governed by non-abelian gauge theories and general relativity. These theories look very different, but recent research has uncovered the “double copy”—an exact correspondence between their mathematical structures. Prof. Chris White reviews its theoretical origins and practical uses, highlighting links to string theory, exotic field theories, and open questions in pure mathematics.

[Prof. Chris White](https://www.seresearch.qmul.ac.uk/cfp/people/cwhite/) is a theoretical physicist at Queen Mary University of London. He studied at the University of Cambridge, before holding positions in Amsterdam, Durham and Glasgow. His research focuses on theories of particle physics, and their relationship to gravity and beyond. 

Chris White traces the origins and impact of a remarkable new correspondence linking non-abelian gauge theories with general relativity.

The double copy

The double copy: new connections in physics and mathematics

Plato was fascinated by the intricate relationship between science and music. We have explored it, too, in events focusing on the mathematics of the violin and the bagpipes. Now we are delighted to welcome to our rooms a Steinway & Sons grand piano, which is generously being lent to us by the Ukrainian concert pianist Sasha Grynyuk.  

This Steinway Model B grand piano has a distinguished lineage. Before Grunyuk, it belonged to the concert pianist and teacher Noretta Conci-Leech, who studied under Arturo Benedetti Michelangeli. It has also been played by such virtuosi as Evgeny Kissin, Claudio Abbado, Maurizio Pollini, Antonio Pappano and Alfred Brendel. Now it occupies our seminar room, which was once the study of Michael Faraday.

Since it arrived in July, the Faraday grand, as we’re calling it, has been played by, among others, our trustee Ben Delo and, frequently, our fellow Juven Wang. We have also enjoyed recitals from Grynyuk himself and look forward to more in the future. 

The Ukrainian concert pianist Sasha Grynyuk has generously lent us a Steinway grand piano, which was once played by Kissin and Brendel. 

Music to our ears

Matrix models—systems in which randomness and algebraic structure meet—play a central role across theoretical physics and mathematics. Often seen as zero-dimensional analogues of field theories, they also lie at the heart of deep connections linking string theory, integrability, quantum gravity, Yang–Mills theory, combinatorics, geometry, and representation theory.

In this four-part lecture series, Dr Levkovich-Maslyuk provides a guided, pedagogical journey through the subject: starting with motivation and definitions, through reduction to eigenvalue form, to continuum limits and spectral curves, and finally to orthogonal polynomials, phase transitions, and links to two-dimensional gravity. Along the way he sketches the broader vista of loop equations, topological recursion, and integrability. The series offers both newcomers and seasoned theorists a unified and illuminating view of how matrix models continue to shape modern research.

## Event information

This is a four-part lecture series from LonTI. Lectures are on Mondays at 10:30 am in the seminar room at the London Institute, on the second floor of the Royal Institution, followed by drinks and snacks onsite. To register and attend, please visit lonti.weebly.com.

Fedor Levkovich-Maslyuk traces how matrix models reveal striking connections between quantum gravity, string theory and integrability.

Random matrices

Introduction to matrix models

Our universe is chiral—it knows its left from its right. Yet theories with chiral fermions are notoriously difficult to simulate. Dr Rishi Mouland applies powerful symmetry-based techniques to derive the phase diagrams of strongly coupled two-dimensional gauge theories, revealing new, readily simulable models that realise chiral infrared phases and illuminate fresh pathways to understanding the physics of our universe. 

[Dr Rishi Mouland](https://mou.land/) is a postdoc at Imperial College London. He did his PhD at King’s College London followed by postdoctoral research at Cambridge. His interests range from generalised symmetries in strongly coupled gauge theory to quantum gravity and the holographic bootstrap.

Rishi Mouland demonstrates how generalised notions of symmetry can be used in novel ways to probe strongly coupled quantum field theories.

Gapping chiral fermions

Phases of 2d Gauge Theories and Symmetric Mass Generation

In later life, Alexander Grothendieck was captivated by simple graphs encoding holomorphic maps to the sphere. He called them dessins d’enfants—“children’s drawings”. Decades earlier, Gerard ’t Hooft noted that the 1/N expansion in gauge theory mirrors the genus expansion in string theory. Dr Edward Mazenc shows how recent work on AdS/CFT reveals Grothendieck’s insight as the simplest form of gauge–string duality.

[Dr Edward Mazenc](https://www.edwardmazenc.com/) is a research fellow at ETH Zurich. He did his PhD at Stanford and was a Kadanoff Fellow at the University of Chicago. He studied at MIT and Cambridge. His research explores the insights that gauge/string duality offers into the fundamental structure of spacetime.

Edward Mazenc shows how Grothendieck’s dessins d’enfants reveal a deep link between gauge theory, string theory and the AdS/CFT duality.

Strings from graphs

Grothendieck & ’t Hooft: Dessins d’Enfant from AdS/CFT

Integrable models in 1+1 dimensions allow exact solutions of scattering problems and often the complete derivation of spectra. But these models raise a deeper question: what really are the particles being scattering? In low dimensions, unexpected phenomena emerge. Prof. Alessandro Torrielli explores spin and statistics in 1+1 dimensions, delving into one manifestation of this strange behaviour in AdS_3 string theory.
[Alessandro Torrielli](https://www.surrey.ac.uk/people/alessandro-torrielli) is a professor at the University of Surrey. He has held postdoc positions at Padova, HU Berlin, MIT, Utrecht and York. His research interests focus on quantum integrable systems, particularly those appearing in the context of the AdS/CFT correspondence.

Alessandro Torrielli examines spin, statistics and strange particle behaviour in 1+1-dimensional integrable models and AdS_3 string theory.

Integrable statistics

Integrable models, spin and statistics

In 1739, Euler devised the Tonnetz, a lattice to visualise harmonic relations in music. In this talk, Prof. Konstanze Rietsch revisits Euler’s Tonnetz from a modern point of view, exploring Tonnetze on tiled surfaces. She presents examples on triangulated tori related to crystallographic reflection groups, as well as a diatonic case tied to finite geometry, yielding elegant new visualisations of chord progressions.

[Konstanze Rietsch](https://www.kcl.ac.uk/people/konstanze-rietsch) is a professor at King’s College London. She works on the geometry of flag varieties and is also interested in total positivity, a theory that allows many geometric objects occurring in Lie theory to be defined, in some sense, over the positive real numbers.

Konstanze Rietsch explores Euler’s Tonnetz through the lens of modern geometry, revealing new links between music, symmetry and harmony.

Tiling and Tonnetze

Generalising Euler’s Tonnetz

Dr Stephen Wolfram is one of the most restless and original talents in science. Since publishing his first paper in particle physics at just 15, he has created the pioneering software Mathematica, launched the knowledge engine WolframAlpha and developed a radical new framework for fundamental physics.

In this event, Dr Wolfram sits down with our director Thomas Fink and science writer Ananyo Bhattacharya to talk about the big questions. What are the deepest challenges facing theorists today? How should science be organised and communicated? And how might AI-assisted discovery transform maths and physics?

The evening offers a rare opportunity to learn about Dr Wolfram’s intellectual journey and ambitions for the future, as he reflects on his decades-long pursuit of new kinds of science, from cellular automata to his Physics Project to computational insights into life and learning. There will also be time for audience questions and discussion over drinks. 

## Event information

The event takes place on Monday 13 October at the London Institute for Mathematical Sciences, which is on the second floor of the Royal Institution. The event is limited to 80 people and is by invitation only. The interview will start at 4:00pm in our Faraday seminar room, followed by Q&A at 5:00pm. At 5:45pm we will have drinks and canapes with the speaker into the evening.

<a href="https://www.youtube.com/embed/8SD9WgPCZ28?si=Xf5TIxWk7SZw-hX8">Watch the event</a>

Theoretical physicist and innovator Stephen Wolfram discusses the big questions facing science with the London Institute and its guests.

Meet Stephen Wolfram

The latest advances in quantum computing are pushing the limits of our ability to describe and simulate out-of-equilibrium dynamics of quantum systems. Dr Alexey Milekhin introduces powerful theoretical tools to address these problems, focusing on the Sachdev–Ye–Kitaev model and the emerging framework of “entanglement in time”, an information-theoretic approach designed to probe dynamical properties of quantum systems.

[Dr Alexey Milekhin](https://pa.as.uky.edu/users/ami426) is an assistant professor at the University of Kentucky. He has a PhD from Princeton University and did postdocs at UC Santa Barbara and Caltech. His work focuses on statistical mechanics and the dynamics of many-body quantum systems, including quantum gravity.

Alexey Milekhin explores how the Sachdev–Ye–Kitaev model and “entanglement in time” can reveal new ways of understanding quantum dynamics.

Entanglement in time

Quantum dynamics meets quantum information

Since the discovery of the thermodynamics of black holes, a key challenge has been uniting statistical mechanics with gravity and quantum information. Prof. Ginestra Bianconi proposes a new “Gravity from Entropy” action for gravity, with a Lagrangian given by the geometric quantum relative entropy. This framework recovers Einstein’s equations in the low-energy, small-curvature limit and predicts modified gravity beyond.

[Ginestra Bianconi](https://webspace.maths.qmul.ac.uk/g.bianconi/) is a professor at Queen Mary University of London, an APS Fellow and member of the European Academy of Sciences. She is recognised for pioneering work in statistical mechanics and theoretical physics, especially on how topology shapes dynamics in complex networks.

Ginestra Bianconi illustrates her novel approach to quantum gravity, which is grounded in statistical mechanics and information theory.

Gravity from entropy

The history of “artificial intelligence” is the history of an overhyped intellectual brand that has only very recently come to signify a set of deployable technologies with broad application and clear, if somewhat horrifying, purposes. Since its debut in 1955 the AI brand has been attached to a rotating cast of technologies with only loose connections to each other or to cognition, none of which has yet come close to delivering on the promise of creating computer systems with human-like intelligence. One AI insider characterized the story of AI as “the history of failed ideas.” Yet in the process of failing, early AI researchers made vital but incidental contributions to the development of computer technology and computer science.

In this seminar, Thomas Haigh explores where the AI brand came from, why it was so attractive to researchers and sponsors, and how artificial intelligence institutionalised as a subfield of computer science through research labs, curricula, textbooks and professional associations. Haigh also documents continuities and discontinuities between our own moment and earlier cycles of AI hype and disillusionment.

## Event information

The event takes place on Tuesday 7 October at the London Institute for Mathematical Sciences, which is on the second floor of the Royal Institution. To book a place, register [here](https://tally.so/r/n04qXZ).

Thomas Haigh traces the rise of AI as an overhyped brand, from failed ideas to today’s powerful technologies and their unsettling impact.

AI’s history of hype

Artificial Intelligence: the brand that wouldn’t die

The story of science is often told as a series of flashes of insight, enjoyed by heroic figures such as the Royal Institution’s Sir Humphry Davy and Michael Faraday. Yet in reality, innovation is rarely so simple or dramatic.

Drawing on examples from the history of the Royal Institution, as well as insights from his recent book, *Like: The Button that Changed the World*, London Institute Trustee Martin Reeves makes an original case for how scientific breakthroughs really happen. He demonstrates that most are not the result of eureka moments, but a combination of iteration, collaboration and, strangest of all, serendipity. With the aid of vivid demonstrations in the tradition of the Royal Institution, he explains why this does not just mean surrendering to chance. On the contrary, he hones in on the mathematical basis for serendipity—hidden patterns in the history of discovery—and shares the strategies that innovative businesses and research centres use to harness it.

## Event information
This event takes place in the historic lecture theatre of the Royal Institution. Tickets for the talk may be purchased [here](https://www.rigb.org/whats-on/science-serendipity-how-innovation-really-works). London Institute guests, who don’t need to buy tickets, are invited to join the speaker for drinks after the talk in our private rooms on the second floor of the Royal Institution.

In the Royal Institution’s lecture theatre, Martin Reeves reveals the startling truth about how innovation happens in science and technology.

How innovation works

The science of serendipity: how innovation really works

Prof. Mark Gross discusses the notion of scattering diagrams, a powerful means of encoding often very complex wall-crossing data in a wide range of geometric problems. Originally developed in the foundational work of Kontsevich and Soibelman, scattering diagrams have since emerged in many different contexts, including mirror symmetry, cluster algebras, wall-crossing for moduli spaces of sheaves and theoretical physics.

[Prof. Mark Gross](https://www.dpmms.cam.ac.uk/person/mg475) is a pure mathematician at Cambridge University. He did his PhD at UC Berkeley and has held posts at Cornell, Warwick, and UC San Diego. He is renowned for his work on mirror symmetry which has profoundly influenced algebraic, tropical and differential geometry.

Prof. Mark Gross explores how scattering diagrams are a powerful tool for capturing wall-crossing data in many diverse mathematical contexts.

Surveying scattering

Wall-crossing and scattering diagrams in geometry and beyond

Symmetry is a powerful organising principle, enabling remarkably precise, all-order predictions about the behaviour of quantum systems. Dr Christian Copetti explains how generalised symmetries act on boundary conditions and defects, and uses these ideas to constrain key features of (1+1)d scattering amplitudes, such as crossing symmetry, and shows how ultraviolet defects may be screened by bulk degrees of freedom.

[Dr Christian Copetti](https://www.maths.ox.ac.uk/people/christian.copetti) is a postdoc at Oxford University. He did his PhD at IFT in Madrid and then held a research position at SISSA in Trieste. His recent work spans generalized symmetries, defect dynamics, S-matrix bootstrap, and topological constraints in quantum field theories. 

Christian Copetti from Oxford University shows how generalised symmetries guide quantum systems, shaping boundary conditions and defects.

Defects and scattering

Symmetry constraints on defects and scattering amplitudes

Prof. Darryl Holm shows how geometric mechanics uses Lie–Noether symmetries of Hamilton’s principle to derive momentum maps and Euler–Poincaré equations, with variables that evolve by coadjoint motion. This motion imparts common features to their solutions, demonstrating how geometric mechanics offers a way to study symmetry breaking and the multi-scale challenges arising in modern investigations of dynamics in nature.

[Prof. Darryl Holm](https://profiles.imperial.ac.uk/d.holm/about) is a professor of applied mathematics at Imperial College London. His main research interests lie in nonlinear science and most of his work is based on Lie symmetry reduction of Hamilton's principle. He is particularly interested in emergent singular phenomena.

Prof. Darryl Holm explores how geometric mechanics links symmetry-breaking to dynamics, revealing patterns in nature’s complex systems.

Mechanics in a box

Geometric mechanics in a box

Madhuparna Das from the University of Exeter explores a key challenge in the field of artificial intelligence: the automation of mathematical discovery. She introduces HypothesiX, an AI agent that creates novel mathematical conjectures by blending formal reasoning from Lean’s Mathlib with the creative power of Large Language Models. She demonstrates its potential in pure mathematics and explores additional applications.

[Madhuparna Das](https://experts.exeter.ac.uk/35716-madhuparna-das) is an EPSRC Doctoral Fellow at the University of Exeter, supervised by Prof. Nigel Byott. Before her PhD, she did a masters by research at Exeter under Prof. Kyle Pratt and Dr Gihan Marasingha. She works on probabilistic number theory and additive combinatorics.

Madhuparna Das presents an AI agent automating novel mathematical conjecture discovery by integrating Lean’s Mathlib with LLMs’ creativity.

Automated conjectures

Automated conjecture formulation

Prof. Misha Rudnev explains how the long-standing Erdős distinct distance conjecture was resolved in 2010 by Larry Guth and Nets Katz using a combination of tools that were well beyond earlier approaches. Reviewing the methodology, which drew on 19th-century geometry and early 20th-century algebraic topology, Prof. Rudnev discusses some results and a plethora of still wide open questions that followed from their work.

[Prof. Misha Rudnev](https://research-information.bris.ac.uk/en/persons/misha-rudnev) is a professor of mathematics at the University of Bristol. He studied applied mathematics and physics at the Moscow Engineering Physics Institute and did his PhD at Caltech. His research focuses on problems in geometric, arithmetic and additive combinatorics.

Prof. Misha Rudnev from the University of Bristol shows how algebraic geometry helped settle a famous discrete geometry conjecture of Erdős

Erdős and topology

A few helpful interventions from baby algebraic geometry to “hard Erdős questions”

Artificial intelligence is no longer confined to crunching numbers—it is beginning to propose original theorems, sketch proofs and reveal new and unexpected patterns in the abstract world of mathematics. Speaking in the iconic lecture theatre of the Royal Institution, Prof. Yang-Hui He—one of the pioneers of AI-assisted discovery— explores how machine learning is transforming both the practice and philosophy of mathematical research.

Drawing on his own leading-edge work, alongside insights from a recent gathering in Berkeley where mathematicians challenged a powerful AI chatbot to solve problems designed to resist automation, Prof. He traces the emergence of a new form of mathematical exploration. Describing his AI-assisted discovery, with colleagues, of “murmuration” patterns in elliptic curves, Prof. He shows how, by fusing human intuition with computational power, this partnership is reshaping research and redefining the creative boundaries of the field.

## Event information
This event takes place in the historic lecture theatre of the Royal Institution. Tickets for the talk or the live stream may be purchased [here](https://www.rigb.org/whats-on/mathematics-rise-machines). London Institute guests are invited to join the speaker for drinks after the talk in our private rooms on the second floor of the Royal Institution. 

In the Royal Institution’s lecture theatre, Prof. Yang-Hui He reflects on how growing AI-human collaboration is shaping the future of maths.

Maths in the age of AI

Mathematics: the rise of the machines?

Prof. Zhengcheng Gu from the Chinese University of Hong Kong gives an analytical construction of the fixed point tensors of a 2D rational CFT and provides a concrete example by using several models to compute the scaling dimensions explicitly. He shows that the construction of the fixed point tensors is closely related to a strange correlator, where the holographic picture and generalised symmetries naturally emerge.

Prof. Zhengcheng Gu describes the construction of a fixed-point tensor network and its generalised symmetries in conformal field theory.

CFT tensor network

Fixed-point tensor network construction and generalised symmetry for conformal field theory

Symmetries play a central role in mathematics, linking algebra and geometry. Groups and algebras of symmetries provide geometric realisations of respective abstract structures, while their algebraic properties lead to unexpected geometric insights. In this session, three speakers showcase the rich interplay between these two worlds.

First, Prof. Travis Schedler of Imperial College outlines a programme to classify crepant resolutions of moduli spaces—especially Nakajima quiver varieties—revealing new structures beyond the projective case.

Next, Prof. Evgeny Feigin from Tel-Aviv University describes the geometry of the graph closure of a birational map from projective space to a Grassmannian, including its fibres and embeddings into projectivized cyclic representations of a degenerate Lie algebra.
Finally, Prof. Konstanze Rietsch of King’s College London explores new tropical versions of parametrisations for totally positive Toeplitz matrices, offering a unified perspective on their roles in representation theory and mirror symmetry, and connecting them to the quantum cohomology of flag varieties and canonical bases.

## Event information

These talks take place in the seminar room of the London Institute, on the second floor of the Royal Institution. There will be a short coffee break between talks and a longer pause to allow participants to have lunch.

## Programme

- *10:00am* Arrival & Coffee
- *10:30am* Prof. Travis Schedler: Crepant resolutions of moduli spaces and quiver varieties
- *11:40am* Prof. Evgeny Feigin: Birational maps to Grassmannians and poset polytopes
- *13:00pm* Lunch
- *13:30pm* Prof. Konstanze Rietsch: A tropical Edrei theorem

Three leading experts show how the idea of symmetry forms key interfaces between algebra and geometry through the lens of their recent work.

Where two worlds meet

Speakers

Symmetries in algebra and geometry

As Camille Jordan noted in 1870, problems in enumerative geometry have associated Galois groups, just as univariate polynomials do. Despite this pedigree, the subject lay dormant for a century, with systematic investigations of such Galois groups starting only in the past 15 years. Prof. Frank Sottile of Texas A&M University discusses recent advances in this area, describing the current directions and open problems.

Prof. Frank Sottile of Texas A&M outlines the history and the state of the art of a keystone topic at the interface of algebra and geometry.

Enumerative Galois

Galois groups in enumerative geometry

Prof. Ed Segal of UCL discusses derived equivalences and autoequivalences arising from wall-crossing phenomena on Calabi-Yau toric varieties. Mirror symmetry relates these to monodromy around the Gelfand–Kapranov–Zelevinsky's discriminant locus. He conjectures that intersection multiplicities in the discriminant equal the multiplicities appearing in semi-orthogonal decompositions, proving the conjecture in some cases.

Ed Segal from UCL will talk about semi-orthogonal decompositions of derived categories of toric varieties, coming from wall-crossing in GIT.

Discriminants & physics

Discriminants and semi-orthogonal decompositions

The Special Relationship between America and Britain has never been more special than in science. Yet now that the number of scientists looking to leave America is on the rise, what is Britain doing to support them? In a recent [article](https://lims.ac.uk/perspectives/the-most-valuable-cargo/) in *The Spectator*, the Director of the London Institute, Dr Thomas Fink, argued that we should create new scientific posts earmarked for Americans, and view the coming wave of talent not as a prospective win for Britain but as part of the long-term scientific alliance between our two countries.

In this event, Prof. Thomas Rosenbaum, the President of Caltech, will sit down with James Arroyo OBE, the Director of the Ditchley Foundation, for a conversation about how British science can respond to recent proposed cuts to the government funding of science in America. The discussion will be chaired by Dr Fink. There will be time for questions from guests, which will include Caltech alumni, members of the London Institute, science journalists, and others.

## Event information

The event takes place on Tuesday 24 June at the London Institute for Mathematical Sciences, which is on the second floor of the Royal Institution. It starts at 6:30pm.

## Programme

- *6:30pm* Arrival and drinks.
- *7:10pm* Introduction by Thomas Fink.
- *7:15pm* Presentation by Thomas F. Rosenbaum, followed by a chat between him and James Arroyo about how Britain can support America’s scientists. The conversation will be chaired by Thomas Fink.

The President of Caltech chats with the Director of the Ditchley Foundation about how Britain should respond to US science funding cuts.

Supporting US scientists

The Special Relationship between America and Britain has never been more special than in science. That relationship is now being put to the test. According to *Nature*, the number of scientists looking to leave America has recently risen by a third. The question is: what is Britain doing to support them? In a recent article in *The Spectator*, the Director of the London Institute, Thomas Fink, banged the drum for creating new scientific posts that are earmarked for Americans. 

 This event is first and foremost for Caltech alumni and postdocs. Prof. Thomas F. Rosenbaum, the President of Caltech, will begin proceedings with an update on Caltech news. There will then be a conversation between Prof. Rosenbaum and James Arroyo OBE, the Director of the Ditchley Foundation, about how British science should respond to recent proposed cuts to the American state funding of science. The discussion will be chaired by Thomas Fink and will be open to questions from guests.

## Event information

The event takes place on Tuesday 24 June at the London Institute for Mathematical Sciences, which is on the second floor of the Royal Institution. Please come at 6:30 pm for drinks beforehand.

## Programme

- *6:30pm* Arrival and drinks.
- *7:10pm* Introduction by Thomas Fink.
- *7:15pm* Presentation by Thomas F. Rosenbaum, followed by a chat between him and James Arroyo about how Britain can support America’s scientists. The conversation will be chaired by Thomas Fink.

Caltech alumni gather at the London Institute to catch up on Caltech news and hear a discussion on how Britain can help American science. 

Caltech in London

Ageing is thought to be an inevitable consequence of breakdowns in how genetic information is processed. But mounting experimental evidence suggests aging can be slowed. To resolve this, Dr Thomas Fink, Director of the London Institute, derives a mortality equation that governs the dynamics of an evolving population with a given maximum age. His solution shows that programmed ageing cannot confer a long-term benefit.

Thomas Fink unveils a mathematical model showing programmed aging cannot be favoured by natural selection, even in a shifting environment.

The mortality equation

Martin Reeves, Senior Partner and Managing Director at the Boston Consulting Group and Trustee of the London Institute, took up the Great Highland bagpipe during the coronavirus pandemic. In this talk and performance, he delves into the noble history and mathematical structure of the instrument. With lyrical insight and expert playing, Mr Reeves shows why the bagpipe is as rich in logic as it is in tradition and sound.

Martin Reeves explores the surprising harmony between the music and maths of the Great Highland bagpipe—complete with a live demonstration.

The mathematical piper

Prof. Michael Douglas of the Center of Mathematical Sciences and Applications at Harvard explores the frontiers of artificial general intelligence, which some experts now anticipate within 2–3 years. Drawing lessons from past milestones—such as when computers surpassed humans in chess—he discusses the development of mathematical copilots and conceptual systems that could soon enable autonomous, machine-led research.

Prof. Michael Douglas examines how advances in AI may soon lead to autonomous systems capable of making genuine mathematical discoveries.

AI for discovery

AI in math and theoretical physics

Prof. Joseph Conlon from Oxford University will explore the largely unconstrained epoch between inflation and nucleosynthesis, spanning more than 30 orders of magnitude in time. String cosmology suggests this era may include moduli-dominated phases—such as kination, tracker, and matter epochs—and he introduces a novel percolation-based scenario for the formation of cosmic string networks in the very early universe.

Prof. Joseph Conlon outlines how string theory suggests new equations of state that may describe the physics of the very early universe.

Early universe strings

String theory and the early universe

Artificial Intelligence is revolutionising our understanding of life. The DeepMind programme tackling the protein folding problem, AlphaFold, ushered in a new era for protein structure prediction and earned its creators last year’s Nobel Prize in Chemistry. But that was just the beginning.

Speaking in the historic lecture theatre of the Royal Institution, Dr Mikhail Burtsev gives a tour of the leading-edge biological applications of AI, including his own, that are now making complex biological insights more accessible than ever before. AI chatbots such as ChatGPT are trained on human language, but these new AI models are instead fed billions of real DNA sequences, allowing them to perform astonishing feats like designing new biological molecules—or even whole new bacterial genomes. Their ultimate goal is to solve perhaps the most fundamental problem in all of biology—reading and understanding life’s genetic blueprint from beginning to end.

## Event information

This event, which includes research supported by the Khodorkovsky Foundation, takes place in the lecture theatre at the Royal Institution. London Institute guests are invited to join the speaker after for drinks in our private rooms.

Mikhail Burtsev explains how artificial intelligence is helping to decipher genomes in the Royal Institution’s iconic lecture theatre.

Decoding life with AI

Dr Simon Telen leads the numerical algebraic geometry group at the Max Planck institute for Mathematics in the Sciences in Leipzig. He studies toric amplitudes—rational functions inspired by the scattering amplitudes of particle physics but associated to arbitrary simplicial polyhedral fans. He describes the algebraic properties of such amplitudes and their zero loci, exploring their Fano schemes and singular loci.

Simon Telen presents his discovery of a new connection between polynomials inspired by particle physics and classical algebraic geometry.

Geometry meets physics

Mr Pinardin is a PhD student at the University of Edinburgh. He addresses the problem of describing the linearizable subgroups of the plane Cremona group, the group of birational self-maps of the projective plane. Drawing on work with Drs Arman Sarikyan and Egor Yasinsky, Mr Pinardin gives a complete solution to this problem, equivalent to the question of G-equivariant rationality, over the field of complex numbers.

Antoine Pinardin presents a complete description of the linearisable subgroups of the plane Cremona group over the field of complex numbers.

Linearising groups

Linearisation problem for finite subgroups of the plane Cremona group

Dr Matthew Buican is a Reader in theoretical physics at Queen Mary University of London. He describes a universal relevant deformation that takes local unitary 3d N=4 superconformal field theories to topological quantum field theories, explaining, for example, how Abelian mirror symmetry is related to generalisations of level-rank duality, as well as some results that arise as a result of ’t Hooft anomaly matching. 

Dr Matthew Buican details how a universal deformation takes 3d N=4 superconformal field theories to 3d topological quantum field theories.

Conformal to topological

A universal connection between 3d N=4 SCFTs and 3d TQFTs

Symmetry plays a fundamental role in quantum systems, shaping their dynamics, enforcing selection rules and enabling the development of new algorithms for nascent quantum computers. In recent years, novel forms of symmetry, known as generalised global symmetries, have been discovered in a wide range of quantum systems. These include non-invertible symmetries and higher-group symmetries, which go beyond traditional notions of symmetry and provide new insights into the structure and behavior of quantum theories.

In this series of four lectures, Dr Hsin will explore the role of these symmetries in various quantum systems and their applications, such as their ability to constrain low-energy dynamics. The lectures will examine examples from quantum mechanics, gauge theories and lattice models, focusing on ordinary symmetries, higher-form symmetries and non-invertible symmetries, shedding light on their profound impact in modern physics.

## Event information

This is a four-part lecture series from LonTI. Lectures are on Mondays at 10:30 am in the Tyndall seminar room at the London Institute, on the second floor of the Royal Institution, followed by drinks and snacks onsite. To register and attend, please visit lonti.weebly.com.

Dr Po-Shen Hsin introduces generalised symmetries in quantum systems and explores their roles in dynamics, constraints and applications.

Quantum symmetries

Symmetries in quantum systems

In a session co-chaired by Prof. Kevin Buzzard of Imperial College London and Prof. Richard Hill of University College London, researchers and PhD students discuss their projects in the area of formal proof verification in Lean. The meeting includes visitors from Imperial, UCL, the University of Cambridge and Google DeepMind as well as the London Institute, fostering collaboration across a wide swathe of mathematics.

Mathematicians across London share their work on the formalisation of mathematics using the AI proof-assistant computer language Lean.

London learns Lean

Two seminars discuss new applications of AI to quantum theory. Prof. Koji Hashimoto of Kyoto University shows how a neural network can generate arbitrary Feynman path integrals as a consequence of the universal approximation theorem. Afterwards, Dr Akio Tomiya of Tokyo Woman's Christian University introduces a transformer architecture designed for lattice QCD that outperforms existing gauge covariant neural networks.

In two consecutive talks, Prof. Koji Hashimoto and Dr Akio Tomiya discuss applying machine learning to problems in quantum field theory.

AI for QFT

Prof. Konstantinos Zoubos from the University of Pretoria will explain how Lie groupoids and their twists are the appropriate framework to discuss the true symmetries of N=2 supersymmetric orbifold gauge field theories in the planar limit. These hidden symmetries provide an explanation for certain non-trivial relations between QFT observables and point to possible integrable structures associated to these theories.

Prof. Konstantinos Zoubos will use Lie groupoids and their twists to uncover hidden symmetries of supersymmetric orbifold field theories.

Groupoids do the twist

Hidden symmetries of orbifold field theories

Dr Bhavik Mehta is research fellow at Imperial College London, where he works with Prof. Kevin Buzzard, an expert on formal proof verification. Dr Mehta did his PhD at Cambridge under the supervision of Prof. Timothy Gowers and later worked on Google DeepMind’s AlphaProof, which formulates problems in Lean. In a series of talks at the London Institute, he shows how Lean can verify proofs and even help find them.

Dr Bhavik Mehta from Imperial College London gives an overview of Lean, the proof-assistant computer language used to formalize mathematics.

Co-piloting proofs

Dr Matthew Yu is a postdoc at the University of Oxford’s Mathematical Institute. He describes how topological theories that are fermionic in nature can be rigorously axiomatised in low dimensions with additional structure to accommodate their relevant physical properties. Prior to the talk, London Institute Fellow Dr Juven Wang will join Dr Yu for a discussion on the physical and mathematical context of the problem.

Dr Matthew Yu explains how fermionic topological quantum field theories can be given a categorical description in 3+1-dimensional spacetime.

Fermionic TQFTs

Categorical description of fermionic topological theories in 3+1d

Quantum Chromodynamics has been a profound source of inspiration for theoretical physicists, driving the development of key concepts such as string theory, effective field theories, instantons, anomalies, and lattice gauge theories. In this four-part lecture series, Dr Guerrieri will explore two distinct regimes of Quantum Chromodynamics—its infrared and ultraviolet limits—and the theoretical tools used to study them.

In the infrared regime, where perturbative techniques break down, Effective Field Theories provide a powerful framework. Here, Dr Guerrieri will introduce the pion EFT as a tool to study non-linearly realized symmetries and soft theorems. In the ultraviolet regime, where Quantum Chromodynamics becomes amenable to perturbative analysis, he will discuss the Operator Product Expansion and renormalization group equations, focusing on their application to deep inelastic scattering, a cornerstone in the discovery of quarks and gluons.

## Event information

This is a four-part lecture series from LonTI. Lectures are on Mondays at 10:30 am in the Tyndall seminar room at the London Institute, on the second floor of the Royal Institution, followed by drinks and snacks onsite. To register and attend, please visit lonti.weebly.com.

Andrea Guerrieri presents tools to probe QCD in its two limits, including pion effective theories and perturbative approaches to scattering.

Exploring QCD’s limits

Exploring the infrared and ultraviolet regimes of QCD​

Dr Alex Davies leads Google DeepMind’s initiative for AI and mathematics. In a discussion with our scientists and staff, he gives his take on AlphaGeometry, which solves hard but known problems, and the possibilities for AI-assisted discovery of new conjectures. He also considers the scope and limits of automated theorem proving, and how the human mind makes shortcuts that machines must spell out pedantically. 

Dr Alex Davies of Google DeepMind leads an interactive discussion about AI-assisted mathematical discovery and automated theorem proving.

Automating maths

Prof. Alexander Migdal, a member of the Institute for Advanced Study and formerly at Princeton and the Landau Institute, presents an exact solution to the Navier-Stokes equations for incompressible fluid flow in the context of decaying turbulence. He introduces the framework of the Euler ensemble, which maps turbulent dynamics onto discrete states represented by regular star polygons with rational vertex angles.

Prof. Alexander Migdal presents an infinite dimensional manifold of exact solutions to the Navier-Stokes equations for decaying turbulence.

Solving Navier-Stokes

An exact solution to the Navier-Stokes equations for decaying turbulence

In 1974, Stephen Hawking calculated that black holes emit particles, eventually evaporating away completely. This was the origin of the black hole information paradox, in essence a conflict between quantum theory, which demands that information on particle interactions cannot be lost, and general relativity, which predicts that once a particle crosses the event horizon, no information can ever escape.

In this four-part series, Dr Tarek Anous will give a technical introduction to the paradox. Beginning with a review of quantum path integrals, he will outline the laws of black hole thermodynamics before deriving the Unruh effect, which predicts that a detector with a uniformly accelerated observer measures a temperature related to the observer’s proper acceleration. This will be followed by a session on classical and quantum information theory. The series concludes with a toy model of the paradox and a review of what is left to understand.

### Event information

This is a four-part lecture series from LonTI. Lectures are on Mondays at 10:30 am in the Tyndall seminar room at the London Institute, on the second floor of the Royal Institution, followed by drinks and snacks onsite. To register and attend, please visit [lonti.weebly.com](https://lonti.weebly.com/).


Dr Tarek Anous introduces the 50-year-old black hole information paradox and discusses some of the questions that have yet to be answered.

Black hole paradox

An introduction to the black hole information paradox

In this seminar, Dr Wang will explore key problems in high energy theoretical physics. First, he will discuss the puzzle of why there are three families of quarks and leptons in the Standard Model. He will argue that a dimensional reduction of the Standard Model to a 2-dimensional conformal field theory with chiral central charge c-=0 mod 24 is both modular invariant and framing anomaly free. This result, he will show, is constrained by the Hirzebruch signature theorem, gravitational Chern-Simons theory, and 3 E8 quantum Hall states.

Secondly, Dr Wang will propose a new model of unification constructed from a mod 16 nonperturbative global anomaly cancellation that adds a symmetry-extended anomalous topological quantum field theory to the Standard Model. With this fresh approach to physics beyond the Standard Model, Dr Wang will address long-standing questions relating to the properties of neutrinos, the composition of Dark Matter and the cause of leptogenesis.

Dr Juven Wang proposes novel solutions to open problems in high-energy phenomenology via new analogies from modern ultra quantum matter.

Ultra Unification

Ultra Unification: ultra quantum matter and physics beyond the Standard Model

Simon Norton, who died in February 2019, is best remembered by mathematicians for his remarkable contributions to group theory. A child prodigy, Norton earned a First in mathematics from the University of London while he was still studying at Eton College.

Later, at the University of Cambridge, he would work with John Conway, co-authoring the ATLAS of Finite Groups, the definitive catalogue of different types of symmetry. The pair’s paper on monstrous moonshine, published in 1979, proposed an unexpected deep connection between the monster group and the j-function. Seemingly far-fetched, the conjecture was proved in 1992 by Richard Borcherds and is recognised as one of the great unifying conjectures in modern mathematics.

In the second Simon Norton Lecture, Prof. Leonard Soicher will explain what the monster is and its importance before describing Norton’s research on the internal structure of the group and its subgroups. He will also discuss his work with Norton and Conway on the projective plane presentation for the bimonster. We are grateful to Simon’s family for their generous support of this lecture.

## Event information

The event takes place on Wednesday 12 February at the London Institute for Mathematical Sciences, which is on the second floor of the Royal Institution. To book a place, [register here](https://tally.so/r/wdQKDK). 

## Programme

- *5:30pm* Arrival and drinks, Old Post Room
- *6:00pm* Prof. Yang-Hui He, Introduction, Tyndall seminar room
- *6:10pm* Prof. Leonard Soicher, “Simon and the Monster”
- *7:10pm* Drinks and canapes, Old Post room

In the second Simon Norton Lecture, Prof. Leonard Soicher will convey the mystery and the magic of the monster group to a general audience.

A friendly monster

The London Institute was founded in 2011 and incorporated on 10 February. This marked the birth of Britain’s only independent research organisation in the physical sciences. The date is also the feast day of St Scholastica, who lived in Italy in the 6th century and is the patron saint of learning and Benedictine nuns.

One of the few surviving stories about St Scholastica is that one night, after her brother St Benedict had dined with her, he rose to leave. She prayed to God to make it rain, so he would be compelled to stay and they might continue talking. So it came to pass. St Scholastica is therefore indelibly associated with evenings filled with good conversations, which continue into the night.

To celebrate our founding and our belief in the value of community, we hold an annual St Scholastica’s Feast in our rooms. This formal dinner is for our scientists and staff and a handful of distinguished guests. It takes place on a Friday near the day of our incorporation.

## Event information

The dinner is at 7 o’clock on Friday, 14 February in our rooms on the second floor of the Royal Institution. Dress is black tie. We meet in the Old Post Room, then head to dinner in the Faraday Room and dessert in the Bragg Room, followed by drinks in the Old Post Room.

We hold an annual formal dinner in our rooms, to mark the anniversary of our founding and affirm our belief in the importance of community.

St Scholastica’s Feast

Our Christmas party takes place in our rooms in the Royal Institution on the first Friday of December. It’s a chance to celebrate the contributions of our supporters and collaborators—which is why most attendees are from outside the Institute.
Because our financial year ends in December, our Christmas party is also a chance to take stock of the past year and set out our vision for the next.

Attending our 2024 Christmas party are one High Commissioner, two British knights, three of our Trustees, four science writers, five major donors, six Alexanders, seven RI members, eight tech upstarts, nine Erdös 3-ers, ten LIMS Fellows, eleven rock climbers, and twelve Russian and Ukrainian theorists.

Among the 78 attendees are the Director of the International Centre for Mathematical Sciences, the Director of the Royal Institution, and members of the Khodorkovsky and Sakharov foundations, who have supported our programme of fellowships for Russian and Ukrainian researchers.

## Event information

Our Christmas party is on Friday, 6 December, from 6 o’clock until late. It is held in the London Institute’s Faraday Room and Old Post Room, on the second floor of the Royal Institution. The party is for members of the Institute and their guests and those who have supported us.

Our Christmas party is an opportunity to celebrate our supporters and collaborators, review the past year, and set our plans for the future.

Christmas party

Combinatorial geometry serves as a bridge between various areas of mathematics, such as discrete and algebraic geometry, combinatorics, and algebra, facilitating the transfer and abstraction of ideas across these fields and their applications. In particular, over the last decade, an explosive exchange of ideas between algebraic geometry and combinatorial convexity has led to breakthroughs in both disciplines, the resolution of many landmark conjectures, Fields Medals, and even new entries in the mathematics subject classification.

The two talks at our meeting survey these advances and present an up-to-date overview of combinatorial geometry to the broader mathematical community. It is a pleasure for the London Institute to welcome the speakers, whose contributions to the field have largely shaped its landscape. The presence of combinatorial geometry in the research of many mathematicians and physicists at the Institute—spanning topics from algebraic geometry and representation theory to mirror symmetry and beyond—illustrates its central, connecting role across mathematics.

## Event information

The collquium takes place on Monday 18 November at the London Institute for Mathematical Sciences, which is on the second floor of the Royal Institution in Mayfair. Please enter the door under "Ri" flags and take the stairs.

The London Institute will host two talks by leading experts, surveying recent advances at the intersection of geometry and combinatorics.

Matroids are combinatorial structures that track “independence” relations on a set. A key example is the linear independence of vectors in a vector space. While not all matroids arise from a vector space, those that don't often exhibit surprising algebraic behavior as if they do. Breakthroughs over the last decade have introduced a suite of tools from, and inspired by, algebraic geometry to prove inequalities for matroids, including the 'matroid Hodge theory' developed by Adiprasito, Huh, Katz, and others. I'll begin by motivating matroids and aim to conclude with enough about my work in progress with Andy Berget to illustrate how its central tool differs from matroid Hodge theory.

Matroid inequalities from algebraic geometry

The factorization problem asks under what conditions two birationally isomorphic varieties, X and Y, share a common iterated smooth blowup, Z. Oda specifically conjectured that this holds for toric varieties. We provide an affirmative answer if the blowups are allowed to be at rationally smooth centers, solving a weighted version of Oda's conjecture and addressing a separate conjecture of Alexander in PL topology.

The Oda conjecture

Combinatorial geometry

Combinatorial geometry colloqioum

Conjectures can inspire new branches of pure mathematics and theoretical physics. They usually come from spotting patterns and applying instinct. Recently, there has been a surge of interest in using automated pattern detection to help humans form conjectures. Because in mathematics there are no coincidences, mathematical data is immune from the false positives and false negatives that plague physical measurement.

In this two-day workshop, the London Institute brings together physicists and mathematics to explore how AI can speed up theoretical research. The topics addressed range from geometry to string theory to representation theory.

This is the fourth in the series of annual DANGER workshops (Data, Numbers, Geometry and Representation theory). The series was created by Alexander Kasprzyk from Nottingham University, Thomas Oliver from Westminster University, and Yang-Hui He from the London Institute. This is a hybrid workshop. Those unable to attend in person can join online via Zoom.

## Event information

This workshop takes place on Thursday 24 and Friday 25 August at the London Institute for Mathematical Sciences, which is on the second floor of the Royal Institution in Mayfair. To register to attend this workshop, please visit the conference [website](https://sites.google.com/view/danger4workshop/home).

## Programme

The London Institute hosts a two-day workshop for theorists to discuss and explore the links between data science, AI and pure mathematics.

Thursday 8 August

Arrival

Proposing good conjectures is at least as valuable as proving theorems. Good conjectures capture our attention and orient our efforts, acting like guide posts on the 'mazy paths to hidden truths' (Hilbert). This talk will touch on three aspects of computer-aided conjecture generation: matching numerical values, symbolic regression and generative models. I will present a Zipf-type law for Physics equations, discuss how genetic algorithms can be used to identify new identities of Rogers-Ramanujan type and present a number of conjectural generating functions for holomorphic line bundle cohomology on certain complex projective varieties.

Computer-aided conjecture generation in maths and physics

Lunch

In this talk, we explore the asymptotic behaviour a certain sequence, which contains the coefficients of a series called the regularized quantum period. This is conjectured to be a complete invariant of Fano varieties and its can be considered as a numerical fingerprint of each Fano variety. We discuss how these results originate from the study of large datasets using data analysis and machine learning techniques and show how they can be used to visualise the landscape of these objects. This is joint work with Tom Coates and Alexander Kasprzyk.

Asymptotic formulae for the regularized quantum period

How can we make sure that a machine learning system gives results as it should, is not biased or is safe to use–as we would like for self-driving cars, for example? We cannot. Not fully. But we can try! This talk will be an incursion in theoretical computer science and formal verification. We will explain ways one can model machine learning systems to try to obtain partial guarantees on them, and how to enforce some safety property.

Why AI works: The spontaneous emergence of a law of parsimony

2 PM, 7 Nov 2025